题目内容
已知椭圆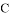 :
: 经过点
经过点 ,离心率为
,离心率为 ,点
,点 为椭圆
为椭圆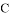 的右顶点,直线
的右顶点,直线 与椭圆相交于不同于点
与椭圆相交于不同于点 的两个点
的两个点 .
.
(Ⅰ)求椭圆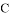 的标准方程;
的标准方程;
(Ⅱ)当 时,求
时,求 面积的最大值;
面积的最大值;
(Ⅲ)若,求证: 为定值.
为定值.
练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
题目内容
已知椭圆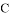 :
: 经过点
经过点 ,离心率为
,离心率为 ,点
,点 为椭圆
为椭圆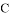 的右顶点,直线
的右顶点,直线 与椭圆相交于不同于点
与椭圆相交于不同于点 的两个点
的两个点 .
.
(Ⅰ)求椭圆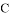 的标准方程;
的标准方程;
(Ⅱ)当 时,求
时,求 面积的最大值;
面积的最大值;
(Ⅲ)若,求证: 为定值.
为定值.
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案