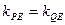题目内容
设抛物线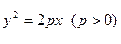
的轴和它的准线交于E点,经过焦点F的直线交抛物线于P、Q
两点(直线PQ与抛物线的轴不垂直),则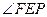
与
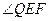的大小关系为 ( )
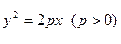的轴和它的准线交于E点,经过焦点F的直线交抛物线于P、Q两点(直线PQ与抛物线的轴不垂直),则
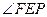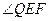与的大小关系为 ( )A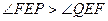． | B． |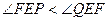
C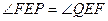． | D．不确定 |
C
向量解法: 由A、F、B共线得
(重要结论),进而得出
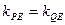
(重要结论),进而得出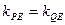
练习册系列答案
相关题目
题目内容
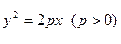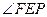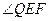的轴和它的准线交于E点,经过焦点F的直线交抛物线于P、Q与的大小关系为 ( )| A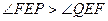． | B． |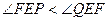
| C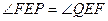． | D．不确定 |
(重要结论),进而得出
时,方程
=kx的解的个数是( )
（
为非零常数）的焦点为
，点
为抛物线
上一个动点，过点
．
与直线
的取值范围；
的取值范围内时，求抛物线截直线所得弦长的最小值。
,焦点为F,一直线
与抛物线交于A、B两点,且
,且AB的垂直平分线恒过定点S(6, 0)
面积的最大值.
按向量
平移后所得抛物线的焦点坐标为___________．
上一定点
，作两条直线分别交抛物线于
，（1）求该抛物线上纵坐标为
的点到其焦点
的距离；（2）当
与
的斜率存在且倾斜角互补时，求
的值，并证明直线
的斜率是非零常数。
的动弦AB长为
,则AB中点M到
轴的最短距离是 ( )
的焦点与双曲线
的右焦点重合,则
的值