题目内容
【题目】已知圆![]() :
:![]() ,定点
,定点![]() ,
,![]() 是圆
是圆![]() 上的一动点,线段
上的一动点,线段![]() 的垂直平分线交半径
的垂直平分线交半径![]() 于
于![]() 点.
点.
(1)求![]() 点的轨迹
点的轨迹![]() 的方程;
的方程;
(2)四边形![]() 的四个顶点都在曲线
的四个顶点都在曲线![]() 上,且对角线
上,且对角线![]() 、
、![]() 过原点
过原点![]() ,若
,若![]() ,求证:四边形
,求证:四边形![]() 的面积为定值,并求出此定值.
的面积为定值,并求出此定值.
【答案】(1)![]() ;(2)证明详见解析,定值为
;(2)证明详见解析,定值为![]() .
.
【解析】
(1)利用椭圆的定义即可得到![]() 点的轨迹
点的轨迹![]() 的方程;
的方程;
(2)不妨设点![]() 、
、![]() 位于
位于![]() 轴的上方,则直线
轴的上方,则直线![]() 的斜率存在,设
的斜率存在,设![]() 的方程为
的方程为![]() ,与椭圆方程联立,求出四边形
,与椭圆方程联立,求出四边形![]() 的面积,即可证明结论.
的面积,即可证明结论.
(1)因为![]() 在线段
在线段![]() 的中垂线上,所以
的中垂线上,所以![]() .
.
所以![]() ,
,
所以轨迹![]() 是以
是以![]() ,
,![]() 为焦点的椭圆,且
为焦点的椭圆,且![]() ,
,![]() ,所以
,所以![]() ,
,
故轨迹![]() 的方程
的方程![]() .
.
(2)不妨设点![]() 、
、![]() 位于
位于![]() 轴的上方,则直线
轴的上方,则直线![]() 的斜率存在,设
的斜率存在,设![]() 的方程为
的方程为
![]() ,
,![]() ,
,![]() .
.
联立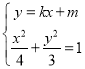 ,得
,得![]() ,
,
则![]() ,
,![]() .①
.①
由![]() ,
,
得![]() .②
.②
由①、②,得![]() .③
.③
设原点到直线![]() 的距离为
的距离为![]() ,
,
![]() ,
,
![]() .④
.④
由③、④,得![]() ,故四边形
,故四边形![]() 的面积为定值,且定值为
的面积为定值,且定值为![]() .
.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目