题目内容
【题目】已知函数 ![]() 的导函数为f'(x).
的导函数为f'(x).
(Ⅰ)判断f(x)的单调性;
(Ⅱ)若关于x的方程f'(x)=m有两个实数根x1 , x2(x1<x2),求证: ![]() .
.
【答案】解:(Ⅰ)f'(x)=x+1﹣(1+lnx)=x﹣lnx(x>0), 令g(x)=x﹣lnx,由 ![]() (x>0),
(x>0),
可得g(x)在(0,1)上单调递减,(1,+∞)上单调递增,
∴f'(x)=g(x)≥g(1)=1>0,
∴f(x)在(0,+∞)上单调递增 …(4分)
(Ⅱ)依题意, 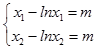 ,相减得
,相减得 ![]() ,
,
令 ![]() (t>1),则有
(t>1),则有 ![]() ,
, ![]() ,
,
欲证 ![]() 成立,
成立,
只需证 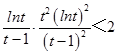 成立,
成立,
即证 ![]() 成立,
成立,
即证  成立,
成立,
令 ![]() (x>1),只需证
(x>1),只需证 ![]() 成立,
成立,
令 ![]() (x>1),
(x>1),
即证x>1时,F(x)>0成立 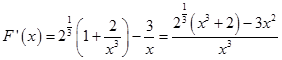 ,
,
令 ![]() (x>1),
(x>1),
则 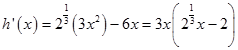 (x>1),
(x>1),
可得h(x)在 ![]() 内递减,在
内递减,在 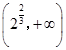 内递增,
内递增,
∴ 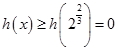 ,
,
∴F'(x)≥0,
∴F(x)在(1,+∞)上单调递增,
∴F(x)>F(1)=0成立,故原不等式成立
【解析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(Ⅱ)欲证 ![]() 成立,问题转化为证
成立,问题转化为证 ![]() 成立,即证
成立,即证 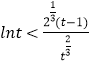 成立,根据函数的单调性证明即可.
成立,根据函数的单调性证明即可.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.

【题目】某县共有户籍人口60万人,该县60岁以上、百岁以下的人口占比13.8%,百岁及以上的老人15人.现从该县60岁及以上、百岁以下的老人中随机抽取230人,得到如下频数分布表:
年龄段(岁) | [60,70) | [70,80) | [80,90) | [90,99) |
人数(人) | 125 | 75 | 25 | 5 |
(1)从样本中70岁及以上老人中采用分层抽样的方法抽取21人进一步了解他们的生活状况,则80岁及以上老人应抽多少人?
(2)从(1)中所抽取的80岁及以上的老人中,再随机抽取2人,求抽到90岁及以上老人的概率;
(3)该县按省委办公厅、省人民政府办公厅《关于加强新时期老年人优待服务工作的意见》精神,制定如下老年人生活补贴措施,由省、市、县三级财政分级拨款. ①本县户籍60岁及以上居民,按城乡居民养老保险实施办法每月领取55元基本养老金;
②本县户籍80岁及以上老年人额外享受高龄老人生活补贴.
(a)百岁及以上老年人,每人每月发放345元生活补贴;
(b)90岁及以上、百岁以下老年人,每人每月发放200元的生活补贴;
(c)80岁及以上、90岁以下老年人,每人每月发放100元的生活补贴.
试估计政府执行此项补贴措施的年度预算.
