Question

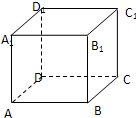如图，在棱长为a的正方体A₁B₁C₁D₁-ABCD中，异面直线AB与A₁D₁所成的角等于（　　）

• A．

  π

  6

• B．

  π

  4

• C．

  π

  3

• D．

  π

  2

Answer 1

分析：欲求异面直线所成角，只需平移异面直线中的一条，是它们成为相交直线，则相交直线所成角即为异面直线所成角，再求出该角即可．

解答：解：∵在正方体A₁B₁C₁D₁-ABCD中，A₁D₁∥AD，∴AB与AD所成角∠DAB即为异面直线AB与A₁D₁所成的角．
∵∠DAB=

π

2

，∴异面直线AB与A₁D₁所成的角等于

π

2

．
故选D．

点评：本题主要考查异面直线所成角的求法，关键是把异面直线所成角转化为平面角．