题目内容
4.长方体的体积公式为V长=Sh,柱体的体积公式为V柱=Sh,锥体的体积公式为V椎=$\frac{1}{3}$Sh.若给出原理“两等高的几何体,若被平行于底面的平面所截的截面积相等,则这两个几何体的体积相等”.试用上述知识解释球的体积公式V球=$\frac{4}{3}$πR3.分析 由祖暅原理的内容的提示此题可先观察V圆锥、V半球、V圆柱这三个量(等底等高)之间的不等关系,再构造一个参照体,这样的参照体我们可以用圆柱内挖去一个圆锥构造出,接下来利用祖暅原理证明猜想.
解答  解:我们先推导半球的体积.为了计算半径为R的半球的体积,我们先观察V圆锥、V半球、V圆柱这三个量(等底等高)之间的不等关系,
解:我们先推导半球的体积.为了计算半径为R的半球的体积,我们先观察V圆锥、V半球、V圆柱这三个量(等底等高)之间的不等关系,
可以发现V圆锥<V半球<V圆柱,即$\frac{1}{3}$πR3<V半球<πR3,根据这一不等关系,我们可以猜测V半球=$\frac{2}{3}$πR3,并且由猜测可发现V半球=V圆柱-V圆锥.
下面进一步验证了猜想的可靠性.关键是要构造一个参照体,这样的参照体我们可以用圆柱内挖去一个圆锥构造出,如图所示.下面利用祖暅原理证明猜想.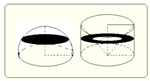
证明:用平行于平面α的任意一个平面去截这两个几何体,截面分别为圆面和圆环面.
如果截平面与平面α的距离为l,那么圆面半径r=$\sqrt{{R}^{2}-{l}^{2}}$,圆环面的大圆半径为R,小圆半径为r.
因此S圆=πr2=π(R2-l2),
S环=πR2-πl2=π(R2-l2),∴S圆=S环.
根据祖暅原理,这两个几何体的体积相等,即V半球=$π{R}^{2}•R-\frac{1}{3}π{R}^{2}•R$=$\frac{2}{3}$πR3,
所以V球=$\frac{4}{3}$πR3.
点评 本题考查祖暅原理、几何体的体积,考查转化思想,是基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
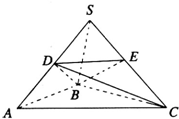 如图,在三棱锥S-ABC中,SB⊥底面ABC,且SB=AB=2,BC=$\sqrt{6},∠ABC=\frac{π}{2}$,D、E分别是SA、SC的中点.
如图,在三棱锥S-ABC中,SB⊥底面ABC,且SB=AB=2,BC=$\sqrt{6},∠ABC=\frac{π}{2}$,D、E分别是SA、SC的中点.