题目内容
2．函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+2x-8，x＞0}\\{-x-2，x＜0}\end{array}\right.$，g（x）=3x-1则使不等式f（g（x））≥0成立的区间为（ ）| A． | [1，+∞） | B． | [1n3，+∞） | C． | [1，ln3] | D． | [-1，ln3） |
分析 先求出f（x）≥0的解集，进而结合指数函数的图象和性质，可得使不等式f（g（x））≥0成立的区间．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+2x-8，x＞0}\\{-x-2，x＜0}\end{array}\right.$，
令f（x）≥0，
则x≥2，或x≤-2，
又∵g（x）=3x-1＞-1，
故不等式f（g（x））≥0成立时，g（x）=3x-1≥2，
即x≥1，
即使不等式f（g（x））≥0成立的区间为[1，+∞），
故选：A
点评 本题考查的知识点是分段函数的应用，指数函数的图象和性质，一次函数和二次函数的图象和性质，难度不大，属于中档题．
练习册系列答案
相关题目
12．若M点的极坐标为$（{2，\frac{5π}{6}}）$，则M点的直角坐标是（ ）
| A． | （-$\sqrt{3}$，1） | B． | （-$\sqrt{3}$，-1） | C． | （$\sqrt{3}$，-1） | D． | （$\sqrt{3}$，1） |
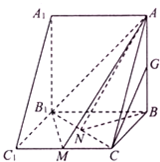在直三棱柱ABC-A1B1C1中，已知BC=CC1=AB，AB⊥BC，点M，N，G分别是CC1，B1C，AB的中点．