题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若![]() 的图像与
的图像与![]() 轴围成直角三角形,求
轴围成直角三角形,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)分3段去绝对值解不等式组,再求并;
(2)将y=f(x)去绝对值写出分段函数,根据其图象与x轴围成直角三角形,转化为(a﹣1)(a+1)=﹣1或(a+1)(1﹣a)=﹣1,可解得.
(1)当a=2时,不等式f(x)>1,即|x+1|﹣|2x﹣3|>1,
当x≤﹣1时,原不等式可化为﹣x﹣1+2x﹣3>1,解得x>5,因为x≤﹣1,所以此时原不等式无解;
当﹣1![]() 时,原不等式可化为x+1+2x﹣3>1,解得x>1,所以1<x
时,原不等式可化为x+1+2x﹣3>1,解得x>1,所以1<x![]() ;
;
当x![]() 时,原不等式可化为x+1﹣2x+3>1,解得x<3,所以
时,原不等式可化为x+1﹣2x+3>1,解得x<3,所以![]() x<3.
x<3.
综上,原不等式的解集为{x|1<x<3}.
(2)因为![]() ,所以
,所以![]() ,所以
,所以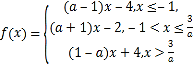 ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,
当![]() 时,要使得
时,要使得![]() 的图象与
的图象与![]() 轴围成直角三角形,
轴围成直角三角形,
则![]() ,解得
,解得![]() ,舍去;
,舍去;
当![]() 时,
时,![]() 的图象与
的图象与![]() 轴不能围成三角形,不符合题意,舍去;
轴不能围成三角形,不符合题意,舍去;
当![]() 时,要使得
时,要使得![]() 的图象与
的图象与![]() 轴围成直角三角形,
轴围成直角三角形,
则![]() ,解得
,解得![]() ,因为
,因为![]() ,所以
,所以![]() .
.
综上,所求![]() 的值为
的值为![]() .
.

【题目】“工资条里显红利,个税新政入民心”.随着2019年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段.某![]() 从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁-35岁(2009年-2018年)之间各年的月平均收入
从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁-35岁(2009年-2018年)之间各年的月平均收入![]() (单位:千元)的散点图:(注:年龄代码1-10分别对应年龄26-35岁)
(单位:千元)的散点图:(注:年龄代码1-10分别对应年龄26-35岁)
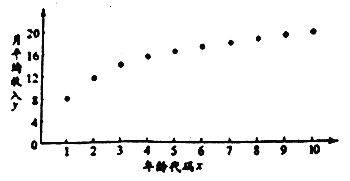
(1)由散点图知,可用回归模型![]() 拟合
拟合![]() 与
与![]() 的关系,试根据有关数据建立
的关系,试根据有关数据建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)如果该![]() 从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入视为月收入,根据新旧个税政策,估计他36岁时每个月少缴纳的个人所得税.
从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入视为月收入,根据新旧个税政策,估计他36岁时每个月少缴纳的个人所得税.
附注:①参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,其中
,其中![]() :取
:取![]() ,
,![]() .
.
②参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为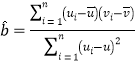 ,
,![]() .
.
③新旧个税政策下每月应纳税所得额(含税)计算方法及税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
缴税 级数 | 每月应纳税所得额(含税) | 税率 | 每月应纳税所得额(含税) | 税率 |
1 | 不超过1500元的都分 | 3 | 不超过3000元的都分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元至55000元的部分 | 30 | 超过35000元至55000元的部分 | 30 |
|
|
|
|
|