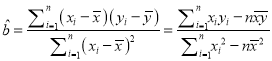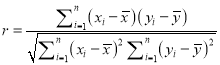题目内容
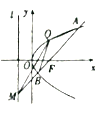
【题目】已知抛物线![]() 焦点为
焦点为![]() ,且
,且![]() ,
,![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点.
两点.
(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)若![]() 为坐标原点,
为坐标原点,![]() 为定值,当
为定值,当![]() 变化时,始终有
变化时,始终有![]() ,求定值
,求定值![]() 的大小;
的大小;
(3)若![]() ,
,![]() ,
,![]() ,当
,当![]() 改变时,求三角形
改变时,求三角形![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意知![]() ,抛物线的方程为
,抛物线的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,联立
,联立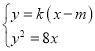 ,
,![]() ,由此利用韦达定理、向量的数量积公式,结合已知条件能求出
,由此利用韦达定理、向量的数量积公式,结合已知条件能求出![]() ;
;
(2)由向量的数量积得![]() ,由此能求出
,由此能求出![]() ;
;
(3)当![]() 时,
时,![]() ,由判别式得
,由判别式得![]() ,由此能求出三角形
,由此能求出三角形![]() 面积的最大值.
面积的最大值.
(1)由题意知![]() ,抛物线的方程为
,抛物线的方程为![]() ,
,
直线![]() 的方程为
的方程为![]() ,联立
,联立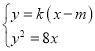 ,消去
,消去![]() 得
得![]() .
.
当![]() 时,设
时,设![]() 、
、![]() ,则
,则![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
![]()
![]() ,解得
,解得![]() ;
;
(2)![]() ,
,![]() ,
,![]() 为定值,当
为定值,当![]() 变化时,始终有
变化时,始终有![]() ,
,
![]() ,解得
,解得![]() 或
或![]() ;
;
(3)当![]() 时,
时,![]() ,由判别式
,由判别式![]() ,得
,得![]() ,
,
则![]()
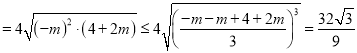 ,
,
![]() 当
当![]() 时,三角形
时,三角形![]() 的面积取最大值
的面积取最大值![]() .
.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
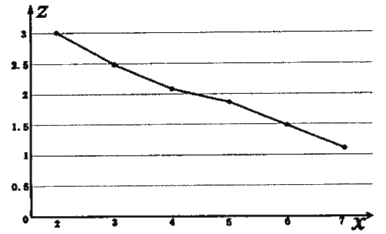
【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,分别记录了4月1日至4月5日每天的昼夜温差与每天100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
温差 | 12 | 11 | 13 | 10 | 8 |
发芽率 | 26 | 25 | 30 | 23 | 16 |
(1)从这5天中任选2天,求至少有一天种子发芽数超过25颗的概率;
(2)请根据4月1日、4月2日、4月3日这3天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)根据(2)中所得的线性回归方程,预测温差为![]() 时,种子发芽的颗数.
时,种子发芽的颗数.
参考公式: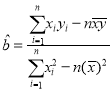 ,
,![]()