Question

【题目】已知曲线C1： (t为参数)曲线C2：＋y2＝4．

(1)在同一平面直角坐标系中，将曲线C2上的点按坐标变换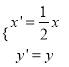后得到曲线C′。求曲线C′的普通方程，并写出它的参数方程；

(2)若C1上的点P对应的参数为t＝π/2，Q为C′上的动点，求PQ中点M到直线C3： (t为参数)的距离的最小值

Answer 1

【答案】（1）x2＋y2＝4， ；（2）.

【解析】试题分析：(1)直接根据坐标变换公式可得曲线C′的方程；(2) 曲线C′的方程的方程化为参数方程，根据参数方程可设M(-2+cosθ，2+sinθ)，直线参数方程化为普通方程，利用点到直线的距离公式结合辅助角公式及三角函数的有界性可得结果.

试题解析:（1） 由得到①

将①代入＋y2＝4，得＋y′2＝4，即x′2＋y′2＝4.

因此椭圆＋y2＝4经伸缩变换后得到的曲线方程是x2＋y2＝4.

它的参数方程为

当t=π/2时，P（-4,4），Q（2cosθ,2sinθ）,故M(-2+cosθ，2+sinθ)

曲线C3：为直线x-2y+8=0,

M到C3的距离d=|(-2+cosθ)-2(2+sinθ)+8|=|cosθ-2sinθ+2|=|cos(θ+α)+2|

从而tanα=2时d的最小值为|-+2|=.