题目内容
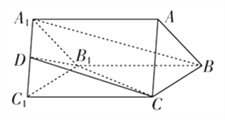
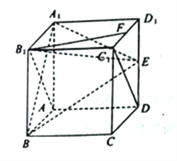
【题目】如图,在长方体![]() 中,
中, ![]() 分别为
分别为![]() 的中点.
的中点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)证明: ![]() 平面
平面![]() ;
;
(3)若正方体棱长为1,求四面体![]() 的体积.
的体积.
【答案】(1)详见解析;(2) 详见解析;(3) ![]() .
.
【解析】试题分析:(1)要证平面![]() 平面
平面![]() ,即证A1B⊥平面ADC1B1;(2)要证
,即证A1B⊥平面ADC1B1;(2)要证![]() 平面
平面![]() ,即证线线平行;(3)利用等积变换求四面体
,即证线线平行;(3)利用等积变换求四面体![]() 的体积.
的体积.
试题解析:
(1)如图,因为ABCD-A1B1C1D1为正方体,所以B1C1⊥平面ABB1A1.
因为A1B![]() 平面ABB1A1,所以B1C1⊥A1B.
平面ABB1A1,所以B1C1⊥A1B.
因为A1B⊥AB1,B1C1∩AB1=B1,所以A1B⊥平面ADC1B1.
因为A1B![]() 平面A1BE,所以平面ADC1B1⊥平面A1BE
平面A1BE,所以平面ADC1B1⊥平面A1BE
(2)如图,设AB1∩A1B=O,连接EF,OE.
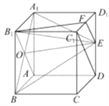
由已知条件得EF∥C1D,且EF= ![]() C1D.B1O∥C1D且B1O=
C1D.B1O∥C1D且B1O= ![]() C1D,
C1D,
所以EF∥B1O且EF=B1O,所以四边形B1OEF为平行四边形,
所以B1F∥OE,
因为B1F平面A1BE,OE![]() 平面A1BE,所以B1F∥平面A1BE
平面A1BE,所以B1F∥平面A1BE
(3) ![]() .
.

 应用题作业本系列答案
应用题作业本系列答案【题目】为了研究家用轿车在高速公路上的车速情况,交通部门随机对50名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在30名男性驾驶员中,平均车速超过![]() 的有20人,不超过
的有20人,不超过![]() 的有10人.在20名女性驾驶员中,平均车速超过
的有10人.在20名女性驾驶员中,平均车速超过![]() 的有5人,不超过
的有5人,不超过![]() 的有15人.
的有15人.
(Ⅰ)完成下面的列联表,并判断是否有![]() 的把握认为平均车速超过
的把握认为平均车速超过![]() 的人与性别有关;
的人与性别有关;
平均车数超过
| 平均车速不超过
| 合计 | |
男性驾驶员人数 | |||
女性驾驶员人数 | |||
合计 |
(Ⅱ)以上述数据样本来估计总体,现从高速公路上行驶的大量家用轿车中随即抽取3辆,记这3辆车中驾驶员为女性且车速不超过![]() 的车辆数为
的车辆数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列和数学期望
的分布列和数学期望
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】(本小题满分12分) 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过![]() ):
):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
|
|
|
|
该社团将该校区在![]() 年
年![]() 天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
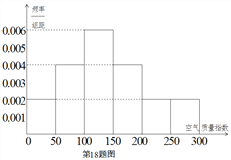
(Ⅰ)请估算![]() 年(以
年(以![]() 天计算)全年空气质量优良的天数(未满一天按一天计算);
天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)该校![]() 年
年![]() 月
月![]() 、
、![]() 日将作为高考考场,若这两天中某天出现
日将作为高考考场,若这两天中某天出现![]() 级重度污染,需要净化空气费用
级重度污染,需要净化空气费用![]() 元,出现
元,出现![]() 级严重污染,需要净化空气费用
级严重污染,需要净化空气费用![]() 元,记这两天净化空气总费用为
元,记这两天净化空气总费用为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.