题目内容
【题目】已知函数
，曲线
的图象在点
处的切线方程为
.
（1）求
，并证明
；
（2）若
对任意的
恒成立，求实数
的取值范围.
【答案】（1）见解析； （2）
.
【解析】
（1）由导数的几何意义，求得
，得到函数的解析式，构造新函数
，利用导数求得函数
的单调性与最值，即可求解；
（2）把
对任意的
恒成立等价于
对任意的
恒成立，
令
，利用导数求得函数
的单调性与最值，即可求解．
（1）根据题意，函数
，则
，则
，
由切线方程
可得切点坐标为
，将其代入
，解得，
故
，则
，
则
，得
，
，函数
单调递减；
，函数单调递增；
所以
，所以
．
（2）由对任意的恒成立等价于对任意的恒成立，
令，
得
，
由（1）可知，当
时，
恒成立，
令
，得
；
，得
，
所以的单调增区间为
，单调减区间为
，
故
，所以
.
所以实数
的取值范围为.
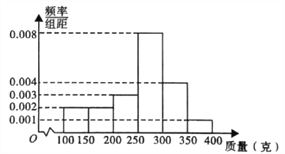
津桥教育计算小状元系列答案【题目】“黄梅时节家家雨”“梅雨如烟暝村树”“梅雨暂收斜照明”……江南梅雨的点点滴滴都流润着浓烈的诗情.每年六、七月份，我国长江中下游地区进入持续25天左右的梅雨季节，如图是江南
镇2009～2018年梅雨季节的降雨量（单位：
）的频率分布直方图，试用样本频率估计总体概率，解答下列问题：
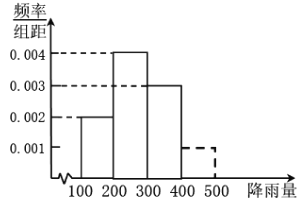
“梅实初黄暮雨深”.请用样本平均数估计镇明年梅雨季节的降雨量；
“江南梅雨无限愁”.镇的杨梅种植户老李也在犯愁，他过去种植的甲品种杨梅，他过去种植的甲品种杨梅，亩产量受降雨量的影响较大（把握超过八成）.而乙品种杨梅2009～2018年的亩产量（
/亩）与降雨量的发生频数（年）如
列联表所示（部分数据缺失）.请你帮助老李排解忧愁，他来年应该种植哪个品种的杨梅受降雨量影响更小？
（完善列联表，并说明理由）.
亩产量\降雨量 |
|
| 合计 |
<600 | 2 | ||
| 1 | ||
合计 | 10 |
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.703 |
（参考公式：
，其中
）
【题目】基于移动互联技术的共享单车被称为“新四大发明”之一,短时间内就风靡全国,带给人们新的出行体验.某共享单车运营公司的市场研究人员为了解公司的经营状况,对该公司最近六个月内的市场占有率进行了统计,结果如下表:
月份 | 2017.8 | 2017.9 | 2017.10 | 2017.11 | 2017.12 | 2018.1 |
月份代码x | 1 | 2 | 3 | 4 | 5 | 6 |
市 场占有率y(%) | 11 | 13 | 16 | 15 | 20 | 21 |
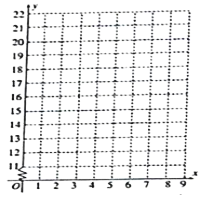
(1)请在给出的坐标纸中作出散点图;
(2)求y关于x的线性回归方程,并预测该公司2018年2月份的市场占有率;
参考公式:回归直线方程为
其中: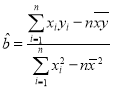
,
