Question

【题目】已知的三个顶点，，，其外接圆为.对于线段上的任意一点，

若在以为圆心的圆上都存在不同的两点，使得点是线段的中点，则的半径的取值范围__________．

Answer 1

【答案】

【解析】分析：求出直线的方程设出点P,N的坐标，结合题意得到点M的坐标，然后根据点都在半径为的上得到关于的方程组，将方程组有解转化为两圆有公共点处理，进而得到关于的不等式恒成立，利用函数的知识求得值域后可得故且，再利用线段与圆无公共点，即直线与圆相离可得，于是可求得．

详解：由题意得直线的方程为．

设点，

∵点是线段的中点，

∴点的坐标为．

又都在半径为的上，

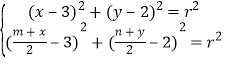∴，即

∵关于的方程组有解，即以为圆心为半径的圆和以为圆心为半径的圆有公共点，

∴，

又

∴对任意的恒成立．

设，则有，

故且．

又线段与圆无公共点，

∴对任意的恒成立，

∴．

综上可得，所以，

即的半径的取值范围是．