题目内容
已知点B在抛物线y2=2x上运动,A(-2,1)为定点,点P内分AB所成比值为2,求P点的轨迹.
P的轨迹是以(-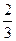 ,
,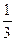 )为顶点,焦点为?(-
)为顶点,焦点为?(-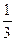 ,
,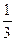 )的抛物线.
)的抛物线.
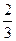 ,
,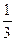 )为顶点,焦点为?(-
)为顶点,焦点为?(-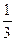 ,
,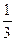 )的抛物线.
)的抛物线.设P(x,y)、B(x0,y0),则y02=2x0.
由已知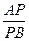 =2,
=2,
所以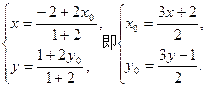
代入y02=2x0,得(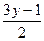 )2=2·
)2=2· .
.
化简得(y-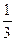 )2=
)2=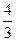 (x+
(x+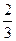 ).
).
故点P的轨迹是以(-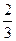 ,
,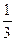 )为顶点,焦点为?(-
)为顶点,焦点为?(-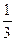 ,
,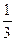 )的抛物线.
)的抛物线.
由已知
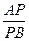 =2,
=2,所以
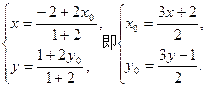
代入y02=2x0,得(
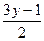 )2=2·
)2=2· .
.化简得(y-
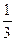 )2=
)2=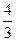 (x+
(x+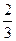 ).
).故点P的轨迹是以(-
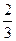 ,
,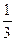 )为顶点,焦点为?(-
)为顶点,焦点为?(-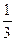 ,
,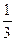 )的抛物线.
)的抛物线.
练习册系列答案
相关题目
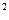 =4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是( )
=4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是( )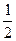 ,则实数m的值为________________.
,则实数m的值为________________. (
(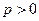 )的焦点为F,经过点 F的直线交抛物线于A、B两点.点C在抛物线的准线上,且BC∥X轴.证明直线AC经过原点O.
)的焦点为F,经过点 F的直线交抛物线于A、B两点.点C在抛物线的准线上,且BC∥X轴.证明直线AC经过原点O.