题目内容
设抛物线
（
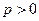）的焦点为F，经过点 F的直线交抛物线于A、B两点．点C在抛物线的准线上，且BC∥X轴．证明直线AC经过原点O．
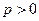（）的焦点为F，经过点 F的直线交抛物线于A、B两点．点C在抛物线的准线上，且BC∥X轴．证明直线AC经过原点O．证明略
因为抛物线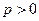（）的焦点为
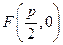，所以经过点F的直线AB的方程可设为
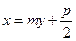，代人抛物线方程得
．
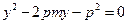若记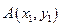
，
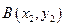，则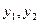
是该方程的两个根，所以
．
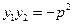因为BC∥X轴，且点C在准线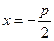
上，所以点C的坐标为
，
故直线CO的斜率为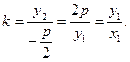
即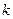
也是直线OA的斜率，所以直线AC经过原点O．
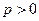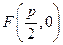（）的焦点为，所以经过点F的直线AB的方程可设为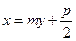，代人抛物线方程得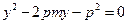．若记
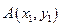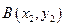，，则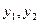是该方程的两个根，所以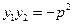．因为BC∥X轴，且点C在准线
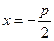上，所以点C的坐标为，故直线CO的斜率为
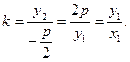
即
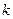也是直线OA的斜率，所以直线AC经过原点O．
练习册系列答案
相关题目
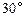角，水流的最高点比喷头高出1.5米，用这种喷水器一次能灌溉多大面积．（精确到十位）
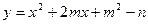焦点坐标为（2001，2002），则它的顶点坐标为 
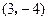抛物线的标准方程。
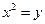交于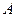
，
两点，它们的横坐标分别为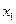
和
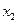，此直线在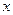
轴上的截距为
，求证：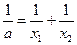
．
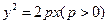的焦点F作倾斜角为
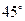的直线交抛物线于A、B两点，若线段AB的长为8，则
________________ 
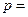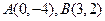，则抛物线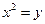
上的点到直线
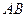的最段距离为 ．
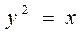的焦点弦AB,求
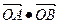的值.