题目内容
【题目】已知双曲线x2－
＝1.
(1)若一椭圆与该双曲线共焦点，且有一交点P(2,3)，求椭圆方程．
(2)设(1)中椭圆的左、右顶点分别为A、B，右焦点为F，直线l为椭圆的右准线，N为l上的一动点，且在x轴上方，直线AN与椭圆交于点M.若AM＝MN，求∠AMB的余弦值；
(3)设过A、F、N三点的圆与y轴交于P、Q两点，当线段PQ的中点为(0,9)时，求这个圆的方程．
【答案】（1）
＝1（2）－
（3）x2＋y2＋2x－18y－8＝0
【解析】(1)∵双曲线焦点为(±2,0)，设椭圆方程为
＝1(a＞b＞0)．
则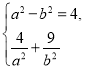
∴a2＝16，b2＝12.故椭圆方程为＝1.
(2)由已知，A(－4,0)，B(4,0)，F(2,0)，直线l的方程为x＝8.
设N(8，t)(t＞0)．∵AM＝MN，∴M
.
由点M在椭圆上，得t＝6.
故所求的点M的坐标为M(2,3)．
所以
＝(－6，－3)，
＝(2，－3)，
·
＝－12＋9＝－3.
cos∠AMB＝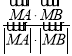
＝
＝－.
(3)设圆的方程为x2＋y2＋Dx＋Ey＋F＝0，将A、F、N三点坐标代入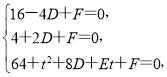，得
得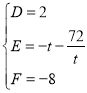
圆的方程为x2＋y2＋2x－
y－8＝0，令x＝0，得y2－
y－8＝0.
设P(0，y1)，Q(0，y2)，则y1,2＝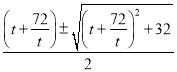
.
由线段PQ的中点为(0,9)，得y1＋y2＝18，t＋
＝18，
此时，所求圆的方程为x2＋y2＋2x－18y－8＝0
智趣寒假作业云南科技出版社系列答案
【题目】某工厂生产甲、乙两种产品所得的利润分别为
和
（万元），事先根据相关资料得出它们与投入资金
（万元）的数据分别如下表和图所示：其中已知甲的利润模型为
，乙的利润模型为
．（
为参数，且
）.
|
|
|
|
|
|
|
|
|
|
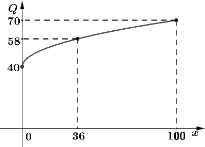
（1）请根据下表与图中数据，分别求出甲、乙两种产品所得的利润与投入资金（万元）的函数模型
（2）今将
万资金投入生产甲、乙两种产品，并要求对甲、乙两种产品的投入资金都不低于
万元．设对乙种产品投入资金
（万元），并设总利润为
（万元），如何分配投入资金，才能使总利润最大？并求出最大总利润．
