题目内容
设m是常数,若 是双曲线
是双曲线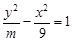 的一个焦点,则m的值为( )
的一个焦点,则m的值为( )
| A.16 | B.34 | C.16或34 | D.4 |
A
解析试题分析:根据双曲线的焦点坐标判断双曲线的焦点位置是解决本题的关键,利用双曲线标准方程中的分母与焦点非零坐标的关系,列出关于m的方程,通过解方程求出m的值解:由于点F(0,5)是双曲线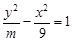
的一个焦点,故该双曲线的焦点在y轴上,从而m>0.从而得出m+9=25,解得m=16.故答案为A
考点:双曲线标准方程
点评:本题考查双曲线标准方程中的分母几何意义的认识,考查双曲线焦点位置与方程的关系、考查学生对双曲线中a,b,c关系式的理解和掌握程度,考查学生的方程思想和运算能力,属于基本题型

练习册系列答案
相关题目
已知动点 在椭圆
在椭圆 上,若
上,若 点坐标为
点坐标为 ,
, ,且
,且 ,则
,则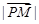 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
抛物线 的焦点F是椭圆
的焦点F是椭圆 的一个焦点,且它们的交点M到F的距离为
的一个焦点,且它们的交点M到F的距离为 ,则椭圆的离心率为
,则椭圆的离心率为
A. | B. | C. | D. |
过双曲线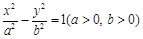 左焦点
左焦点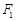 的直线与以右焦点
的直线与以右焦点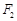 为圆心、
为圆心、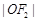 为半径的圆相切于A点,且
为半径的圆相切于A点,且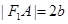 ,则双曲线的离心率为
,则双曲线的离心率为
A.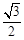 | B.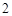 | C.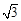 | D.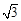 |
如图, 是平面
是平面 的斜线段,
的斜线段, 为斜足。若点
为斜足。若点 在平面
在平面 内运动,使得
内运动,使得 的面积为定值,则动点
的面积为定值,则动点 的轨迹是( )
的轨迹是( )
| A.圆 | B.椭圆 |
| C.一条直线 | D.两条平行直线 |
设 、
、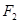 分别是椭圆
分别是椭圆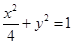 的左、右焦点,
的左、右焦点, 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且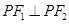 ,则点
,则点 的横坐标为
的横坐标为
A.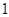 | B.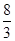 | C.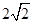 | D.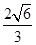 |
若抛物线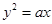 的焦点到准线的距离为4,则此抛物线的焦点坐标为
的焦点到准线的距离为4,则此抛物线的焦点坐标为
A.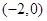 | B.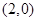 | C.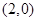 或 或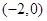 | D.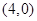 |
 的一条渐近线与抛物线y=x
的一条渐近线与抛物线y=x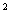 +1 只有一个公共点,则双曲线的离心率为( ).
+1 只有一个公共点,则双曲线的离心率为( ). 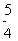
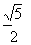
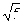
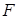 是抛物线
是抛物线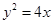 的焦点,准线与
的焦点,准线与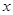 轴的交点为
轴的交点为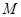 ,点
,点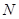 在抛物线上,且
在抛物线上,且 ,则
,则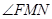 等于( )
等于( )