题目内容
由直线 上的一点向圆
上的一点向圆 引切线,则切线长的最小值( )
引切线,则切线长的最小值( )
A. | B. |
C. | D. |
A
解析试题分析:切线长的最小值是当直线y=x+2上的点与圆心距离最小时取得,圆心(3,-1)到直线的距离为d=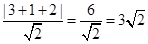 ,圆的半径为
,圆的半径为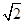 ,故切线长的最小值为
,故切线长的最小值为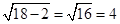 ,则选A。
,则选A。
考点:圆的切线方程的求解
点评:本题考查圆的切线方程,点到直线的距离,是基础题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
已知直线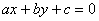 与圆
与圆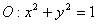 相交于
相交于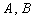 两点,且
两点,且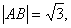 则
则 的值是
的值是
A.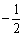 | B.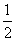 | C.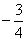 | D.0 |
已知点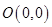 ,
,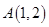 ,
,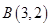 ,以线段
,以线段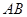 为直径作圆
为直径作圆 ,则直线
,则直线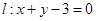 与圆
与圆 的位置关系是
的位置关系是
| A.相交且过圆心 | B.相交但不过圆心 | C.相切 | D.相离 |
已知圆 ,直线
,直线 ,则圆C内任意一点到直线的距离小于
,则圆C内任意一点到直线的距离小于 的概率为( )
的概率为( )
A. | B. | C. | D.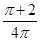 |
直线 与圆
与圆 相交于M、N两点,若
相交于M、N两点,若 ,则k的取值范围为( )
,则k的取值范围为( )
A. | B. | C. | D.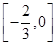 |
已知直线 与圆
与圆 交于
交于 两点,且
两点,且 (其中
(其中 为坐标原点),则实数
为坐标原点),则实数 的值为
的值为
A. | B. | C. 或 或 | D. 或 或 |
设 ,
, ,若直线
,若直线 与圆
与圆 相切,则
相切,则 的取值范
的取值范
围是( )
A. | B. |
C. | D. |
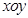 中,圆
中,圆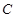 的方程为
的方程为 ,若直线
,若直线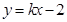 上至少存在一点,使得以该点为圆心,
上至少存在一点,使得以该点为圆心,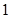 为半径的圆与圆
为半径的圆与圆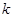 的最大值为
的最大值为 
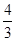


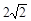 D、8
D、8