题目内容
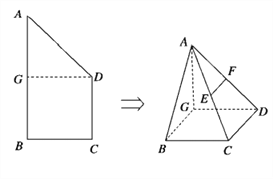
【题目】如图所示,三棱柱A1B1C1﹣ABC的侧棱AA1⊥底面ABC,AB⊥AC,AB=AA1 , D是棱CC1的中点.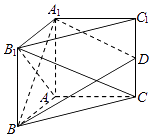
(Ⅰ)证明:平面AB1C⊥平面A1BD;
(Ⅱ)在棱A1B1上是否存在一点E,使C1E∥平面A1BD?并证明你的结论.
【答案】解:(Ⅰ)∵AA1⊥底面ABC,AC平面ABC,∴AA1⊥AC,
又∵AB⊥AC,AA1∩AB=A,∴AC⊥平面ABB1A1,
又∵A1B平面ABB1A1,∴AC⊥A1B,
∵AB=AA1,∴A1B⊥AB1,
又∵AB1∩AC=A,∴A1B⊥平面AB1C,
又∵A1B平面A1BD,∴平面AB1C⊥平面A1BD.
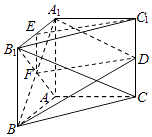
(Ⅱ)当E为A1B1的中点时,C1E∥平面A1BD.下面给予证明.
设AB1∩A1B=F,连接EF,FD,C1E,
∵EF= ![]() AA1,EF∥AA1,且C1D=
AA1,EF∥AA1,且C1D= ![]() AA1,C1D∥AA1,
AA1,C1D∥AA1,
∴EF∥C1D,且EF=C1D,
∴四边形EFDC1是平行四边形,
∴C1E∥FD,又∵C1E平面A1BD,FD平面A1BD,
∴C1E∥平面A1BD.
【解析】(Ⅰ)本小题利用“如果一个平面过另一个平面的一条垂线,那么这两个平面互相垂直”;(Ⅱ)证明一条直线平行于一个平面只需证明在平面内有一条直线与该直线平行即可.
【考点精析】通过灵活运用直线与平面平行的判定和平面与平面垂直的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价为5元,销售单价与日均销售量的关系如图所示.
销售单价/元 | … | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | … |
日均销售量/桶 | … | 480 | 460 | 440 | 420 | 400 | 380 | … |
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
【题目】为了解适龄公务员对开放生育二胎政策的态度,某部门随机调查了90位三十岁到四十岁的公务员,得到如下列联表,因不慎丢失部分数据.
(1)完成表格数据,判断是否有99%以上的把握认为“生二胎意愿与性别有关”并说明理由;
(2)已知15位有意愿生二胎的女性公务员中有两位来自省妇联,该部门打算从这15位有意愿生二胎的女性公务员中随机邀请两位来参加座谈,设邀请的2人中来自省妇联的人数为X,求X的分布列及数学期望E(X).
男性公务员 | 女性公务员 | 总计 | |
有意愿生二胎 | 15 | 45 | |
无意愿生二胎 | 25 | ||
总计 |
P(k2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
附: ![]() .
.