题目内容
设函数f(x)=2|x-1|-|x+2|.
(1)求f(x)≤6的解集.
(2)若f(x)≥m对任意x∈R恒成立,求m的范围.
(1)求f(x)≤6的解集.
(2)若f(x)≥m对任意x∈R恒成立,求m的范围.
(1)∵2|x-1|-|x+2|≤6,
不等式等价于:
或
或
,
等价于
或
或
;
∴不等式的解集为[-2,10];
(2)由(1)知f(x)=
,
当x<-2时,f(x)=4-x>6;
当-2≤x≤1时,f(x)=-3x∈[-3,6];
当x>1时,f(x)=4-x>-3,
∴函数最小值为-3,
∵f(x)≥m对任意x∈R恒成立,
∴m≤-3.
不等式等价于:
|
|
|
等价于
|
|
|
∴不等式的解集为[-2,10];
(2)由(1)知f(x)=
|
当x<-2时,f(x)=4-x>6;
当-2≤x≤1时,f(x)=-3x∈[-3,6];
当x>1时,f(x)=4-x>-3,
∴函数最小值为-3,
∵f(x)≥m对任意x∈R恒成立,
∴m≤-3.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
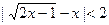
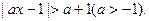
 的定义域为集合A,关于x的不等式
的定义域为集合A,关于x的不等式 的解集为B,求使
的解集为B,求使 的取值范围.
的取值范围. 的解集是 .
的解集是 .