题目内容
设函数f(x)=|x-4|+|x-1|.
(1)求f(x)的最小值;
(2)若f(x)≤5,求x的取值范围.
(1)求f(x)的最小值;
(2)若f(x)≤5,求x的取值范围.
(1)∵f(x)=|x-4|+|x-1|≥|x-4+(1-x)|=3,
∴f(x)min=3;
(2)当x<1时,f(x)=4-x+1-x=5-2x,
∴f(x)≤5?5-2x≤5,
∴0≤x<1;
当1≤x≤4时,f(x)=4-x+(x-1)=3≤5恒成立,
∴1≤x≤4;
当x>4时,f(x)=x-4+x-1=2x-5,
∴f(x)≤5?2x-5≤5,
解得:4<x≤5;
综上所述,x的取值范围为[0,5].
∴f(x)min=3;
(2)当x<1时,f(x)=4-x+1-x=5-2x,
∴f(x)≤5?5-2x≤5,
∴0≤x<1;
当1≤x≤4时,f(x)=4-x+(x-1)=3≤5恒成立,
∴1≤x≤4;
当x>4时,f(x)=x-4+x-1=2x-5,
∴f(x)≤5?2x-5≤5,
解得:4<x≤5;
综上所述,x的取值范围为[0,5].

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
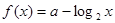 的图象经过点A(1,1),则不等式
的图象经过点A(1,1),则不等式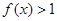 的解集为______.
的解集为______.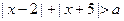 恒成立,则
恒成立,则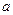 的取值范围是 .
的取值范围是 .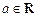 ,则“
,则“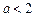 ”是“
”是“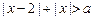 恒成
恒成