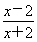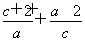Question

若函数f(x)＝(1－x2)(x2＋ax＋b)的图象关于直线x＝－2对称，则f(x)的最大值为________．

 

Answer 1

16

【解析】因为点(1，0)，(－1，0)在f(x)的图象上，且图象关于直线x＝－2对称，所以点(－5，0)，(－3，0)必在f(x)的图象上，所以f(－5)＝(1－25)(25－5a＋b)＝0，f(－3)＝(1－9)(9－3a＋b)＝0，联立，解得a＝8，b＝15，所以f(x)＝(1－x2)(x2＋8x＋15)，即f(x)＝－(x＋1)(x－1)(x＋3)(x＋5)＝－(x2＋4x＋3)(x2＋4x－5)．令t＝x2＋4x＝(x＋2)2－4≥－4，则f(x)＝－(t＋3)(t－5)＝－(t－1)2＋16，当t＝1时，f(x)max＝16.