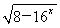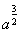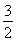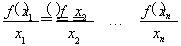题目内容
已知函数g(x)=ax2-2ax+1+b(a≠0,b<1),在区间[2,3]上有最大值4,最小值1,设函数f(x)=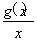 .
.
(1)求a、b的值及函数f(x)的解析式;
(2)若不等式f(2x)-k·2x≥0在x∈[-1,1]时有解,求实数k的取值范围.
(1)a=1,b=0,g(x)=x2-2x+1,f(x)=x+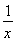 -2.(2)(-∞,1]
-2.(2)(-∞,1]
【解析】(1)g(x)=ax2-2ax+1+b,由题意得
① 得
得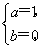
② 得
得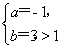 (舍).
(舍).
∴a=1,b=0,g(x)=x2-2x+1,f(x)=x+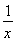 -2.
-2.
(2)不等式f(2x)-k·2x≥0,即2x+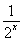 -2≥k·2x,
-2≥k·2x,
∴k≤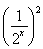 -2·
-2·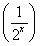 +1.
+1.
设t=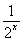 ,则k≤t2-2t+1,∵x∈[-1,1],故t∈
,则k≤t2-2t+1,∵x∈[-1,1],故t∈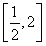 .
.
记h(t)=t2-2t+1,∵t∈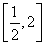 ,∴h(t)max=1,
,∴h(t)max=1,
故所求k的取值范围是(-∞,1]

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目