题目内容
已知函数 ,
, ,
, .
.
(1)若 ,设函数
,设函数 ,求
,求 的极大值;
的极大值;
(2)设函数 ,讨论
,讨论 的单调性.
的单调性.
(1)极大值 ;(2)当
;(2)当 时,
时, 的增区间为
的增区间为 ,
,
当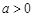 时,
时, 的增区间为
的增区间为 ,减区间为
,减区间为 .
.
解析试题分析:(1)函数求极值分三步:①对函数求导;②令导函数为零求根,判断根是否为极值点;③求出极值;(2)先求导函数,然后利用导数求单调性,在其中要注意对a的分类讨论.
试题解析:(1)当 时,
时, ,定义域为
,定义域为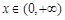 ,
,
则 . 2分
. 2分
令 ,列表: 4分
,列表: 4分
当

1 

+ 0 — 
↗ 极大值 ↘  时,
时, 取得极大值
取得极大值 . 7分
. 7分
(2) ,∴
,∴ . 9分
. 9分
若 ,
, ,
, 在
在 上递增; 11分
上递增; 11分
若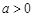 ,当
,当 时,
时, ,
, 单调递增;
单调递增;
当 时,
时, ,
, 单调递减. 14分
单调递减. 14分
∴当 时,
时, 的增区间为
的增区间为 ,
,
当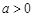 时,
时, 的增区间为
的增区间为 ,减区间为
,减区间为 . 16分
. 16分
考点:(1`)导数求单调性与极值;(2)分类讨论数学思想.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 ,
, .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 在区间
在区间 上是减函数,求
上是减函数,求 的取值范围.
的取值范围. 同时满足以下条件:
同时满足以下条件: 在(0,1)上是减函数,在(1,+∞)上是增函数;
在(0,1)上是减函数,在(1,+∞)上是增函数; 是偶函数;
是偶函数; 的解析式;
的解析式; ,若存在实数x∈[1,e],使g(x)<
,若存在实数x∈[1,e],使g(x)< ,
, ,
,
 ,求曲线
,求曲线 在
在 处的切线方程;
处的切线方程; ,都有
,都有 恒成立,求
恒成立,求 的最小值;
的最小值; ,
, ,若
,若 ,
, 为曲线
为曲线 的两个不同点,满足
的两个不同点,满足 ,且
,且 ,使得曲线
,使得曲线 在
在 处的切线与直线AB平行,求证:
处的切线与直线AB平行,求证:
 x2+6x-a.
x2+6x-a.
 ;
; 在
在 上单调递增;
上单调递增; ,若直线PQ∥x轴,求P,Q两点间的最短距离.
,若直线PQ∥x轴,求P,Q两点间的最短距离.