题目内容
已知函数f(x)满足f(x)=f(π-x),且当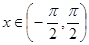 时,f(x)=x+sinx,则( )
时,f(x)=x+sinx,则( )
| A.f(1)<f(2)<f(3) | B.f(2)<f(3)<f(1) |
| C.f(3)<f(2)<f(1) | D.f(3)<f(1)<f(2) |
D
解析试题分析:由已知得函数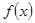 关于
关于 对称,当
对称,当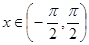 时,
时,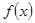 是单调递增函数,当
是单调递增函数,当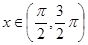 时函数是单调递减函数,比较1,2,3距离对称轴的远近得出
时函数是单调递减函数,比较1,2,3距离对称轴的远近得出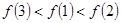 ,故选D.
,故选D.
考点:1.函数的对称性;2.函数的单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义在区间 的奇函数
的奇函数 为增函数,偶函数
为增函数,偶函数 在区间
在区间 的图象与
的图象与 的图象重合,设
的图象重合,设 ,给出下列不等式:
,给出下列不等式:
①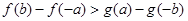 ②
②
③ ④
④ 其中成立的是( )
其中成立的是( )
| A.①与④ | B.②与③ | C.①与③ | D.②与④ |
设偶函数 满足
满足 ,则
,则 ( )
( )
A. | B.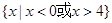 | C. | D. |
对于函数 ,若存在区间
,若存在区间 ,使得
,使得 ,则称函数
,则称函数 为“可等域函数”,区间
为“可等域函数”,区间 为函数
为函数 的一个“可等域区间”.给出下列4个函数:
的一个“可等域区间”.给出下列4个函数:
① ;②
;② ; ③
; ③ ; ④
; ④ .
.
其中存在唯一“可等域区间”的“可等域函数”为( )
| A.①②③ | B.②③ | C.①③ | D.②③④ |
已知函数 (
(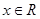 ),则( )
),则( )
A. 必是偶函数 必是偶函数 |
B.当 时, 时, 的图象必须关于 的图象必须关于 直线对称; 直线对称; |
C. 有最大值 有最大值 |
D.若 ,则 ,则 在区间 在区间 上是增函数; 上是增函数; |
函数 则函数
则函数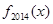 是( )
是( )
| A.奇函数但不是偶函数 | B.偶函数但不是奇函数 |
| C.既是奇函数又是偶函数 | D.既不是奇函数又不是偶函数 |
已知函数 是定义在R上的偶函数, 且在区间
是定义在R上的偶函数, 且在区间 单调递增.若实数
单调递增.若实数 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D.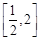 |

 的部分图像可能是( )
的部分图像可能是( )
 的图象大致为( )
的图象大致为( ) 