题目内容
已知函数 (
(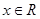 ),则( )
),则( )
A. 必是偶函数 必是偶函数 |
B.当 时, 时, 的图象必须关于 的图象必须关于 直线对称; 直线对称; |
C. 有最大值 有最大值 |
D.若 ,则 ,则 在区间 在区间 上是增函数; 上是增函数; |
D
解析试题分析:在二次函数上加绝对值符号,相当于把原二次函数在 轴下方的图像翻折到上方,原来处于
轴下方的图像翻折到上方,原来处于 轴上方的图像保持不变.
轴上方的图像保持不变.
当 时画图可知
时画图可知 不是偶函数,比如
不是偶函数,比如 就不是偶函数,排除A;
就不是偶函数,排除A;
仅有 无法说明
无法说明 的图像关于
的图像关于 直线对称,比如
直线对称,比如 满足
满足 但画图可知图像并不关于
但画图可知图像并不关于 直线对称,排除B;
直线对称,排除B; 的图像两边向上无限延伸,没有最大值,排除C;
的图像两边向上无限延伸,没有最大值,排除C;
若 ,则函数
,则函数 于
于 轴最多有一个交点,故恒有
轴最多有一个交点,故恒有 ,因此
,因此 ,其对称轴为
,其对称轴为 ,开口向上,因此
,开口向上,因此 在区间
在区间 上是增函数,D正确.
上是增函数,D正确.
考点:1、二次函数图象及变换;2、函数的对称性、单调性与最值.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
若函数 是函数
是函数 的反函数,则
的反函数,则 的值为( )
的值为( )
A. | B. | C.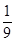 | D.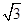 |
已知函数 是定义在
是定义在 上的偶函数,且
上的偶函数,且 ,则下列各式中一定成立
,则下列各式中一定成立
的是( ).
A. | B. |
C. | D.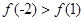 |
已知 ,
, ,规定:当
,规定:当 时,
时,  ;当
;当 时,
时,  ,则
,则 ( )
( )
A.有最小值 ,最大值1 ,最大值1 | B.有最大值1,无最小值 |
C.有最小值 ,无最大值 ,无最大值 | D.有最大值 ,无最小值 ,无最小值 |
已知函数f(x)满足f(x)=f(π-x),且当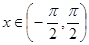 时,f(x)=x+sinx,则( )
时,f(x)=x+sinx,则( )
| A.f(1)<f(2)<f(3) | B.f(2)<f(3)<f(1) |
| C.f(3)<f(2)<f(1) | D.f(3)<f(1)<f(2) |
已知
 ,定义
,定义 ,其中
,其中 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
设函数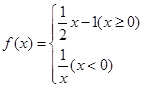 若
若 ,则实数
,则实数 ( )
( )
| A.4 | B.-2 | C.4或 | D.4或-2 |
在实数的原有运算法则中,我们补充定义新运算“⊕”;当a≥b时,a⊕b=a;当a<b时,a⊕b=b2,函数f(x)=(1⊕x)·x(其中“·”仍为通常的乘法),则函数f(x)在[0,2]上的值域为( )
| A.[0,4] | B.[1,4] | C.[0,8] | D.[1,8] |
 :函数
:函数 的图象恒过定点
的图象恒过定点 ;命题
;命题 :若函数
:若函数
 为偶函数,则函数
为偶函数,则函数 的图象关于直线
的图象关于直线 对称,则下列命题为真命题的是( )
对称,则下列命题为真命题的是( )


