题目内容
2.已知圆C经过点A(0,2)和B(2,-2),且圆心C在直线l:x-y+1=0上.(1)求圆C的方程;
(2)若直线m过点(1,4),且被圆C截得的弦长为6,求直线m的方程.
分析 (1)设出圆心的坐标,利用半径相等求得t,进而利用两点的距离公式求得半径,则圆的方程可得.
(2)先看斜率不存在时是否符合.进而看斜率存在时设出直线m的方程,利用点到直线和距离和勾股定理建立等式求得k,则直线的方程可得.
解答 (1)解:设圆心的坐标为(t,t+1),
则有t2+(t-1)2=(t-2)2+(t+3)2,
整理求得t=-3,
故圆心为(-3,-2),r2=t2+(t-1)2=25,
则圆的方程为(x+3)2+(y+2)2=25.
(2)当直线m的斜率不存在时,方程为x=1,被圆截得的弦长2d=2×$\sqrt{25-16}$=6,符合,
当直线的斜率不存在时,设直线m的方程为y-4=k(x-1)整理得,kx-y+4-k=0,
圆心到直线的距离为$\frac{|-3k+2+4-k|}{\sqrt{{k}^{2}+1}}$=$\sqrt{25-9}$=4,求得k=$\frac{5}{12}$.
则直线的方程为$\frac{5}{12}$x-y+$\frac{43}{12}$=0,
综合知直线m的方程为x=1或$\frac{5}{12}$x-y+$\frac{43}{12}$=0.
点评 本题主要考查了直线的圆的问题的综合运用.利用数形结合思想是解决问题的常用办法.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
9.两条平行的直线分别经过点A(3,0),B(0,4),它们之间的距离d满足的条件是( )
| A. | 0<d≤3 | B. | 0<d≤5 | C. | 0<d≤4 | D. | 3<d≤5 |
14.某流程图如图所示,现输入如下四个函数,则可以输出f(x)的是( )


| A. | f(x)=-x2+1 | B. | f(x)=x+$\frac{1}{x}$ | C. | f(x)=lg$\frac{1+x}{1-x}$ | D. | f(x)=$\frac{{2}^{x}+1}{{2}^{x}-1}$ |
11.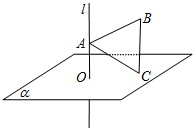 如图,直线l⊥平面α,垂足为O,已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间的最大距离为( )
如图,直线l⊥平面α,垂足为O,已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间的最大距离为( )
 如图,直线l⊥平面α,垂足为O,已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间的最大距离为( )
如图,直线l⊥平面α,垂足为O,已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间的最大距离为( )| A. | $1+\sqrt{2}$ | B. | $2+\sqrt{2}$ | C. | $1+\sqrt{3}$ | D. | $2+\sqrt{3}$ |
12.有3个学习兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |