题目内容
19．已知f（x）=a|x-2|，若f（f（x））＜f（x）恒成立，则a的取值范围为（ ）| A． | a≤-1 | B． | -2＜a＜0 | C． | 0＜a＜2 | D． | a≥1 |
分析 f（f（x））＜f（x）恒成立，可令x=2，解得a＜0，可排除C，D，再由若-2＜a＜0，则可取a=-$\frac{1}{2}$，可令x=6，检验不成立，即可得到答案．
解答 解：f（f（x））＜f（x）恒成立，即有f（f（2））＜f（2），
即为f（0）＜0，即有2a＜0，即a＜0，
故C，D均错，答案为A，B中一个，
若-2＜a＜0，则可取a=-$\frac{1}{2}$，即有f（x）=-$\frac{1}{2}$|x-2|，
当x=6时，f（6）=-2，f（f（6））=f（-2）=-2，
即有f（f（6））=f（6），则B不成立；
由排除法可得A正确．
故选：A．
点评 本题考查函数的恒成立问题，由恒成立思想且为选择题，采取排除法是迅速解题的关键．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
14．某流程图如图所示，现输入如下四个函数，则可以输出f（x）的是（ ）
| A． | f（x）=-x2+1 | B． | f（x）=x+$\frac{1}{x}$ | C． | f（x）=lg$\frac{1+x}{1-x}$ | D． | f（x）=$\frac{{2}^{x}+1}{{2}^{x}-1}$ |
11．
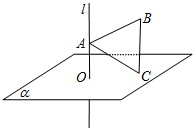如图，直线l⊥平面α，垂足为O，已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动：①A∈l，②C∈α，则B，O两点间的最大距离为（ ）
如图，直线l⊥平面α，垂足为O，已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动：①A∈l，②C∈α，则B，O两点间的最大距离为（ ）| A． | $1+\sqrt{2}$ | B． | $2+\sqrt{2}$ | C． | $1+\sqrt{3}$ | D． | $2+\sqrt{3}$ |