Question

9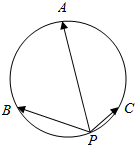．如图，A，B，C是圆O上的三等分点，点P在劣弧$\widehat{BC}$上，且PB=2，PC=1，若实数x，y，z满足x$\overrightarrow{PA}$+y$\overrightarrow{PB}$+z$\overrightarrow{PC}$=$\overrightarrow{0}$．则x：y：z=（　　）

• A． （-1）：2：3
• B． （-3）：2：1
• C． （-2）：3：6
• D． （-6）：3：2

Answer 1

分析 由已知中A，B，C是圆O上的三等分点，点P在劣弧$\widehat{BC}$上，且PB=2，PC=1，利用余弦定理，求出PA长，进而根据实数x，y，z满足x$\overrightarrow{PA}$+y$\overrightarrow{PB}$+z$\overrightarrow{PC}$=$\overrightarrow{0}$．可得：x：y：z．

解答 解：∵点P在劣弧$\widehat{BC}$上，且PB=2，PC=1，
∴BC=$\sqrt{{2}^{2}+{1}^{2}-2×2×1×cos120°}$=$\sqrt{7}$，
则PA=3，
则-2$\overrightarrow{PA}$+3$\overrightarrow{PB}$+6$\overrightarrow{PC}$=$\overrightarrow{0}$．
故x：y：z=（-2）：3：6，
故选：C

点评 本题考查的知识点是向量加减混合运算及其几何意义，其中根据余弦定理求出PA=3，是解答的关键．