题目内容
4．证明：函数f（x）=$\frac{1}{x-1}$在x∈（1，+∞）单调递减．分析 根据减函数的定义，设任意的x1＞x2＞1，然后作差，通分，便可证明f（x1）＜f（x2），这便得出函数f（x）在x∈（1，+∞）上单调递减．
解答 证明：设x1＞x2＞1，则：
$f（{x}_{1}）-f（{x}_{2}）=\frac{1}{{x}_{1}-1}-\frac{1}{{x}_{2}-1}=\frac{{x}_{2}-{x}_{1}}{（{x}_{1}-1）（{x}_{2}-1）}$；
∵x1＞x2＞1；
∴x2-x1＜0，x1-1＞0，x2-1＞0；
∴$\frac{{x}_{2}-{x}_{1}}{（{x}_{1}-1）（{x}_{2}-1）}＜0$；
即f（x1）＜f（x2）；
∴f（x）在x∈（1，+∞）单调递减．
点评 考查减函数的定义，以及根据减函数的定义证明一个函数为减函数的方法和过程，作差的方法比较f（x1）与f（x2）的大小，作差后是分式的一般通分．
练习册系列答案
相关题目
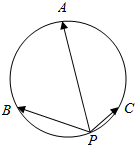如图，A，B，C是圆O上的三等分点，点P在劣弧$\widehat{BC}$上，且PB=2，PC=1，若实数x，y，z满足x$\overrightarrow{PA}$+y$\overrightarrow{PB}$+z$\overrightarrow{PC}$=$\overrightarrow{0}$．则x：y：z=（ ）