题目内容
20.若tanα=tan$\frac{π}{12}$,则$\frac{cos(α-\frac{π}{12})}{sin(α+\frac{π}{12})}$=2.分析 由题意可得α=kπ+$\frac{π}{12}$,k∈Z,代入要求的式子对k分奇数和偶数由诱导公式化简可得.
解答 解:∵tanα=tan$\frac{π}{12}$,∴α=kπ+$\frac{π}{12}$,k∈Z,
∴$\frac{cos(α-\frac{π}{12})}{sin(α+\frac{π}{12})}$=$\frac{coskπ}{sin(kπ+\frac{π}{6})}$,
当k为偶数时,$\frac{coskπ}{sin(kπ+\frac{π}{6})}$=$\frac{1}{\frac{1}{2}}$=2;
当k为奇数时,$\frac{coskπ}{sin(kπ+\frac{π}{6})}$=$\frac{-1}{-\frac{1}{2}}$=2
综上可得$\frac{cos(α-\frac{π}{12})}{sin(α+\frac{π}{12})}$=2,
故答案为:2.
点评 本题考查三角函数求值,涉及分类讨论的思想,属基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
10.将函数f(x)=sin(2x-$\frac{π}{3}$)的图象左移$\frac{π}{3}$,再将图象上各点横坐标压缩到原来的$\frac{1}{2}$,则所得到的图象的解析式为( )
| A. | y=sinx | B. | y=sin(4x+$\frac{π}{3}$) | C. | y=sin(4x-$\frac{2π}{3}$) | D. | y=sin(x+$\frac{π}{3}$) |
8.如果两条异面直线称为“一对”,那么在正方体的十二条棱中共有异面直线( )
| A. | 12对 | B. | 24对 | C. | 36对 | D. | 48对 |
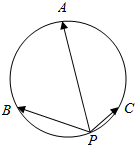 如图,A,B,C是圆O上的三等分点,点P在劣弧$\widehat{BC}$上,且PB=2,PC=1,若实数x,y,z满足x$\overrightarrow{PA}$+y$\overrightarrow{PB}$+z$\overrightarrow{PC}$=$\overrightarrow{0}$.则x:y:z=( )
如图,A,B,C是圆O上的三等分点,点P在劣弧$\widehat{BC}$上,且PB=2,PC=1,若实数x,y,z满足x$\overrightarrow{PA}$+y$\overrightarrow{PB}$+z$\overrightarrow{PC}$=$\overrightarrow{0}$.则x:y:z=( )