题目内容
19.判断并证明函数f(x)=$\frac{1+{x}^{2}}{1-{x}^{2}}$的奇偶性.分析 先求该函数的定义域,判断是否关于原点对称,显然f(-x)=f(x),这样便可判断出该函数的奇偶性.
解答 解:函数的定义域是{x|x≠1且x≠-1};
f(-x)=$\frac{1+(-x)^{2}}{1-(-x)^{2}}=\frac{1+{x}^{2}}{1-{x}^{2}}=f(x)$;
即f(-x)=f(x);
∴该函数为偶函数.
点评 考查函数奇偶性的定义,及判断方法和过程,注意要先求出f(x)的定义域.

练习册系列答案
相关题目
9.如果直线l,m与平面α,β,γ满足:β∩γ=l,m∥l,m?α,则必有( )
| A. | l∥α | B. | α∥γ | C. | m∥β且m∥γ | D. | m∥β或m∥γ |
10.将函数f(x)=sin(2x-$\frac{π}{3}$)的图象左移$\frac{π}{3}$,再将图象上各点横坐标压缩到原来的$\frac{1}{2}$,则所得到的图象的解析式为( )
| A. | y=sinx | B. | y=sin(4x+$\frac{π}{3}$) | C. | y=sin(4x-$\frac{2π}{3}$) | D. | y=sin(x+$\frac{π}{3}$) |
7.直径是2的球的体积为( )
| A. | 4π | B. | 16π | C. | $\frac{32π}{3}$ | D. | $\frac{4π}{3}$ |
8.如果两条异面直线称为“一对”,那么在正方体的十二条棱中共有异面直线( )
| A. | 12对 | B. | 24对 | C. | 36对 | D. | 48对 |
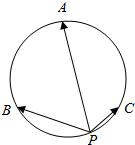 如图,A,B,C是圆O上的三等分点,点P在劣弧$\widehat{BC}$上,且PB=2,PC=1,若实数x,y,z满足x$\overrightarrow{PA}$+y$\overrightarrow{PB}$+z$\overrightarrow{PC}$=$\overrightarrow{0}$.则x:y:z=( )
如图,A,B,C是圆O上的三等分点,点P在劣弧$\widehat{BC}$上,且PB=2,PC=1,若实数x,y,z满足x$\overrightarrow{PA}$+y$\overrightarrow{PB}$+z$\overrightarrow{PC}$=$\overrightarrow{0}$.则x:y:z=( )