题目内容
18.在△ABC中,A,B,C的对边分别是a,b,c,已知$\frac{cosA-\sqrt{3}cosC}{cosB}=\frac{\sqrt{3}c-a}{b}$.(1)求$\frac{c}{a}$的值.
(2)若△ABC的面积为$\sqrt{2}$,cosB=$\frac{\sqrt{3}}{3}$,求b的值.
分析 (1)由$\frac{cosA-\sqrt{3}cosC}{cosB}=\frac{\sqrt{3}c-a}{b}$,利用正弦定理可得:$\frac{cosA-\sqrt{3}cosC}{cosB}$=$\frac{\sqrt{3}sinC-sinA}{sinB}$,化简可得sinC=$\sqrt{3}$sinA,再利用正弦定理即可得出.
(2)由cosB=$\frac{\sqrt{3}}{3}$,可得sinB=$\frac{\sqrt{6}}{3}$.利用S△ABC=$\frac{1}{2}$acsinB=$\sqrt{2}$,可得ac=2$\sqrt{3}$,与$\frac{c}{a}$=$\sqrt{3}$,联立解得即可.
解答 解:(1)∵$\frac{cosA-\sqrt{3}cosC}{cosB}=\frac{\sqrt{3}c-a}{b}$,
由正弦定理可得:$\frac{cosA-\sqrt{3}cosC}{cosB}$=$\frac{\sqrt{3}sinC-sinA}{sinB}$,
化为sin(A+B)=$\sqrt{3}$sin(B+C),
∴sinC=$\sqrt{3}$sinA,
由正弦定理可得:$\frac{c}{a}$=$\frac{sinC}{sinA}$=$\sqrt{3}$.
(2)∵cosB=$\frac{\sqrt{3}}{3}$,∴sinB=$\frac{\sqrt{6}}{3}$.
∵S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}ac×\frac{\sqrt{6}}{3}$=$\sqrt{2}$,∴ac=2$\sqrt{3}$.
又$\frac{c}{a}$=$\sqrt{3}$,联立解得c=$\sqrt{6}$,a=$\sqrt{2}$.
点评 本题考查了正弦定理的应用、和差公式、同角三角函数基本关系式、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案| A. | 12对 | B. | 24对 | C. | 36对 | D. | 48对 |
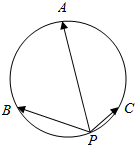 如图,A,B,C是圆O上的三等分点,点P在劣弧$\widehat{BC}$上,且PB=2,PC=1,若实数x,y,z满足x$\overrightarrow{PA}$+y$\overrightarrow{PB}$+z$\overrightarrow{PC}$=$\overrightarrow{0}$.则x:y:z=( )
如图,A,B,C是圆O上的三等分点,点P在劣弧$\widehat{BC}$上,且PB=2,PC=1,若实数x,y,z满足x$\overrightarrow{PA}$+y$\overrightarrow{PB}$+z$\overrightarrow{PC}$=$\overrightarrow{0}$.则x:y:z=( )