题目内容
【题目】选修4-4:极坐标与参数方程
已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() 为参数). 点
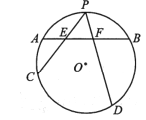
为参数). 点![]() 是曲线
是曲线![]() 上两点,点
上两点,点![]() 的极坐标分别为
的极坐标分别为![]() .
.
(1)写出曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)求![]() 的值.
的值.
【答案】(1)![]() ;(2)4.
;(2)4.
【解析】试题分析:(1)曲线![]() 的参数方程为
的参数方程为![]() ,
, ![]() 为参数),消去参数
为参数),消去参数![]() ,化为普通方程是
,化为普通方程是![]() ,由
,由![]() ,
, ![]() 为参数),曲线
为参数),曲线![]() 的普通方程
的普通方程![]() 可化为极坐标
可化为极坐标![]() ,
, ![]() 为参数);(2)方法1:由
为参数);(2)方法1:由![]() 是圆
是圆![]() 上的两点,且知
上的两点,且知![]() ,
, ![]() 为直径,从而求得
为直径,从而求得![]() .方法2:由两点
.方法2:由两点![]() 化为直角坐标中点的坐标,利用两点间距离公式求得
化为直角坐标中点的坐标,利用两点间距离公式求得![]() 、
、![]() 两点间的距离.
两点间的距离.
试题解析:(1)![]() 曲线
曲线![]() 的参数方程为
的参数方程为![]() ,
, ![]() 为参数),
为参数),
消去参数![]() ,化为普通方程是
,化为普通方程是![]() ;
;
由![]() ,
, ![]() 为参数).
为参数).
![]() 曲线
曲线![]() 的普通方程
的普通方程![]() 可化为极坐标
可化为极坐标![]() ,
, ![]() 为参数).
为参数).
(2)方法1:由![]() 是圆
是圆![]() 上的两点,
上的两点,
且知![]() ,
, ![]() 为直径,
为直径, ![]() .
.
方法2:由两点![]() 化为直角坐标中点的坐标是
化为直角坐标中点的坐标是![]() ,
, ![]() ,
,
![]() 、
、![]() 两点间的距离为
两点间的距离为![]() .
.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
【题目】按照国家环保部发布的新修订的《环境空气质量标准》,规定:PM2.5的年平均浓度不得超过35微克/立方米,国家环保部门在2016年10月1日到2017年1月30日这120天对全国的PM2.5平均浓度的监测数据统计如下:
组别 | PM2.5浓度(微克/立方米) | 频数(天) |
第一组 |
| 32 |
第二组 |
| 64 |
第三组 |
| 16 |
第四组 | 115以上 | 8 |
(1)在这120天中抽取30天的数据做进一步分析,每一组应抽取多少天?
(2)在(1)中所抽取的样本PM2.5的平均浓度超过75(微克/立方米)的若干天中,随机抽取2天,求恰好有一天平均浓度超过115(微克/立方米)的概率.