题目内容
8.设x,y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥x\\ 4x+3y≤12\end{array}\right.$,则$\frac{x+2y+3}{x+1}$的取值范围是( )| A. | [1,5] | B. | [2,6] | C. | [2,10] | D. | [3,11] |
分析 $\frac{x+2y+3}{x+1}$=$\frac{x+1+2(y+1)}{x+1}$=1+2×$\frac{y+1}{x+1}$,设k=$\frac{y+1}{x+1}$,利用z的几何意义进行求解即可.
解答 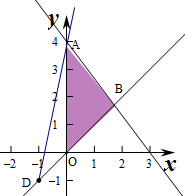 解:作出不等式组对应的平面区域如图:其中A(0,4),B(3,0)
解:作出不等式组对应的平面区域如图:其中A(0,4),B(3,0)
$\frac{x+2y+3}{x+1}$=$\frac{x+1+2(y+1)}{x+1}$=1+2×$\frac{y+1}{x+1}$,
设k=$\frac{y+1}{x+1}$,则k=$\frac{y+1}{x+1}$的几何意义为平面区域内的点到定点D(-1,-1)的斜率,
由图象知BD的斜率最小,AD的斜率最大,
则BD的斜率k=1,AD的斜率为k=$\frac{4+1}{0+1}=5$,
即1≤k≤5,
则2≤2k≤10,
3≤1+2k≤11,
即$\frac{x+2y+3}{x+1}$的取值范围是[3,11],
故选:D
点评 本题主要考查线性规划以及斜率的应用,利用z的几何意义结合分式的性质,利用数形结合是解决本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
16.$\frac{2cos80°+cos160°}{cos70°}$的值是( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\sqrt{3}$ | D. | -$\sqrt{2}$ |
19.指数函数f(x)=(a-1)x(a为常数)在R上单调递减的一个必要不充分条件是( )
| A. | 0<a<1 | B. | 1<a<2 | C. | 1<a<$\frac{3}{2}$ | D. | 0<a<2 |
16.若复数z满足z(1-i)=5+i,则复数z在复平面内对应的点的坐标为( )
| A. | (2,3) | B. | (-2,3) | C. | (2,-3) | D. | (-2,-3) |
13.不等式(x2-2x-3)(x2-4x+4)<0的解集是( )
| A. | {x|x<-1或x>3} | B. | {x|-1<x<3} | C. | {x|x<-3或x>1} | D. | {x|-1<x<2或2<x<3} |
17.若实数a使得方程$2cos({2x+\frac{π}{4}})=a$在$[-\frac{π}{8},\frac{7π}{8}]$有两个不相等的实数根x1,x2,则sin(x1+x2)=( )
| A. | 0 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
