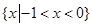题目内容
设二次函数f(x)=ax2+bx+c,函数F(x)=f(x)-x的两个零点为m,n(m<n).
(1)若m=-1,n=2,求不等式F(x)>0的解集;
(2)若a>0,且0<x<m<n<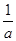 ,比较f(x)与m的大小.
,比较f(x)与m的大小.
(1)若m=-1,n=2,求不等式F(x)>0的解集;
(2)若a>0,且0<x<m<n<
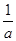 ,比较f(x)与m的大小.
,比较f(x)与m的大小.(1)当a>0时,不等式F(x)>0的解集为{x|x<-1或x>2};当a<0时,不等式F(x)>0的解集为{x|-1<x<2}.
(2)f(x)<m.
(2)f(x)<m.
解:(1)由题意知,F(x)=f(x)-x=a(x-m)(x-n),
当m=-1,n=2时,不等式F(x)>0,
即a(x+1)(x-2)>0.
当a>0时,不等式F(x)>0的解集为{x|x<-1或x>2};当a<0时,不等式F(x)>0的解集为{x|-1<x<2}.
(2)f(x)-m=F(x)+x-m=a(x-m)(x-n)+x-m=(x-m)(ax-an+1),
∵a>0,且0<x<m<n<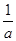 ,
,
∴x-m<0,1-an+ax>0.
∴f(x)-m<0,即f(x)<m.
当m=-1,n=2时,不等式F(x)>0,
即a(x+1)(x-2)>0.
当a>0时,不等式F(x)>0的解集为{x|x<-1或x>2};当a<0时,不等式F(x)>0的解集为{x|-1<x<2}.
(2)f(x)-m=F(x)+x-m=a(x-m)(x-n)+x-m=(x-m)(ax-an+1),
∵a>0,且0<x<m<n<
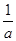 ,
,∴x-m<0,1-an+ax>0.
∴f(x)-m<0,即f(x)<m.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
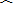
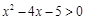 的解集是( )
的解集是( )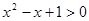
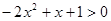
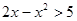
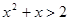
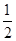 <x<
<x<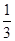 ,则不等式2x2+bx+a<0的解集是________.
,则不等式2x2+bx+a<0的解集是________.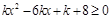 对任意
对任意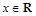 恒成立,则实数
恒成立,则实数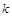 的取值范围为 .
的取值范围为 . 的解集为( )
的解集为( )