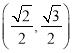题目内容
【题目】如图，已知O为△ABC的重心，∠BOC＝90°，若4BC2＝AB·AC，则A的大小为________．
【答案】
【解析】分别延长BO，CO交AC，AB于D，E，设DO＝x，EO＝y，故BO＝2x，CO＝2y.在Rt△BOC中，BC2＝BO2＋CO2＝4x2＋4y2；在Rt△BOE中，BE2＝BO2＋EO2＝4x2＋y2，故AB2＝4(4x2＋y2)；在Rt△DOC中，DC2＝DO2＋CO2＝x2＋4y2，故AC2＝4(x2＋4y2)．令BC＝a，AB＝c，AC＝b，可知5a2＝b2＋c2①，又4BC2＝AB·AC，即4a2＝cb，
代入①式可知，bc＝b2＋c2－a2，
故由余弦定理得
cos A＝
＝
，
又A∈(0，π)，所以A＝
.
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
【题目】某同学用“五点法”画函数f(x)＝Asin(ωx＋φ) 
在某一个周期内的图象时，列表并填入了部分数据，如下表：
ωx＋φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx＋φ) | 0 | 5 | －5 | 0 |
(1)请将上表数据补充完整，并直接写出函数f(x)的解析式；
(2)将y＝f(x)图象上所有点向左平行移动θ(θ>0)个单位长度，得到y＝g(x)的图象．若y＝g(x)图象的一个对称中心为
，求θ的最小值．
