题目内容
6.若正四面体(四个面都是正三角形的三棱锥)的棱长为6,求它的内切球的表面积.分析 求出正三棱锥的高,求出正三棱锥的全面积和体积,设内切球的半径为r,以球心O为顶点,以棱锥的四个面为底面把正三棱锥分割为四个小棱锥,运用等积法可得球的半径,即可求出球的表面积.
解答 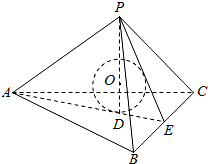 解:由题意,底面外接圆的半径为$\frac{2}{3}$×$\frac{\sqrt{3}}{2}$×6=2$\sqrt{3}$,
解:由题意,底面外接圆的半径为$\frac{2}{3}$×$\frac{\sqrt{3}}{2}$×6=2$\sqrt{3}$,
∴正三棱锥的高为$\sqrt{{6}^{2}-(2\sqrt{3})^{2}}$=2$\sqrt{6}$,
∵正三棱锥的所有棱长都等于6,
则S全=4×$\frac{\sqrt{3}}{4}$×62=36$\sqrt{3}$.
VP-ABC=$\frac{1}{3}$×$\frac{\sqrt{3}}{4}$×36×2$\sqrt{6}$=18$\sqrt{2}$,
设内切球的半径为r,以球心O为顶点,
以棱锥的四个面为底面把正三棱锥分割为四个小棱锥,
则V1+V2+V3+V4=$\frac{1}{3}$rS全=VP-ABC,
∴r=$\frac{3×18\sqrt{2}}{36\sqrt{3}}$=$\frac{\sqrt{6}}{2}$,
∴S球=4πr2=4π×$\frac{6}{4}$=6π.
点评 本题考查正三棱锥与内切球的关系,主要考查球的表面积公式的计算,确定球的半径是关键.

练习册系列答案
相关题目
11.已知在△ABC中,已知b=6,c=6$\sqrt{2}$,B=30°,则解三角形的结果有( )
| A. | 无解 | B. | 一解 | C. | 两解 | D. | 一解或两解 |
15.如图,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )

| A. | $\frac{3}{4}$ | B. | $\frac{8}{3}$ | C. | $\frac{16}{3}$ | D. | 8 |