题目内容
【题目】若函数 
的定义域为R，则实数a的取值范围是 ．
【答案】0≤a≤1
【解析】解：函数 
的定义域为R，∴ 
﹣1≥0在R上恒成立
即x2﹣2ax+a≥0在R上恒成立
该不等式等价于△=4a2﹣4a≤0，
解出0≤a≤1．故实数a的取值范围为0≤a≤1
所以答案是：0≤a≤1
【考点精析】解答此题的关键在于理解函数的定义域及其求法的相关知识，掌握求函数的定义域时，一般遵循以下原则：①
是整式时，定义域是全体实数;②是分式函数时，定义域是使分母不为零的一切实数;③是偶次根式时，定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1,零（负）指数幂的底数不能为零．
练习册系列答案
相关题目
【题目】甲、乙两企业生产同一种型号零件，按规定该型号零件的质量指标值落在
内为优质品.从两个企业生产的零件中各随机抽出了500件，测量这些零件的质量指标值，得结果如下表：
甲企业：
乙企业：
（1）已知甲企业的500件零件质量指标值的样本方差
，该企业生产的零件质量指标值
服从正态分布
，其中
近似为质量指标值的样本平均数
（注：求
时，同一组数据用该区间的中点值作代表），
近似为样本方差
，试根据该企业的抽样数据，估计所生产的零件中，质量指标值不低于71.92的产品的概率.（精确到0.001）
（2）由以上统计数据完成下面
列联表，并问能否在犯错误的概率不超过0.01的前提下，认为“两个分厂生产的零件的质量有差异”.
附注：
参考数据： 
，
参考公式： 
， 
，
.
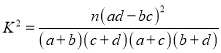
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
