题目内容
【题目】设e为圆锥曲线![]() 的离心率,F为一个焦点,l是焦点所在的对称轴,O是l上距F较近的顶点,又M、N是l上满足
的离心率,F为一个焦点,l是焦点所在的对称轴,O是l上距F较近的顶点,又M、N是l上满足![]() 的两点。求证:对曲线
的两点。求证:对曲线![]() 的过点M的任一条弦AB(A、B为弦的端点),直线l平分NA和NB的一组夹角。
的过点M的任一条弦AB(A、B为弦的端点),直线l平分NA和NB的一组夹角。
【答案】见解析
【解析】
以O为原点、OF为x轴正向建立直角坐标系.
设|OF|=s,则曲线![]() 的方程为
的方程为![]()
又因为OF°0M+ 0F°ON= (1-e)0M°ON已限定M、N异于点O,且当![]() 为椭圆或双曲线时,M、N异于
为椭圆或双曲线时,M、N异于![]() 的中心(否则,有OF=(1-e)0M或OF=(1-e)ON,矛盾).故可设
的中心(否则,有OF=(1-e)0M或OF=(1-e)ON,矛盾).故可设![]() ,知N
,知N![]() .
.
又设直线![]() :
:![]()
其中θ的取值只须保证式②与![]() 有公共点.
有公共点.
将式②代入①并整理,可得![]() .
.
![]() .
.
当点A、B存在时,设所对应的参数分别为![]() ,则
,则![]() ,
,
且由韦达定理知![]() ③
③
由式②可知,![]() .
.
为证直线l平分NA和NB的一组夹角,只须证明直线NA和NB的斜率互为相反数.
这等价于证明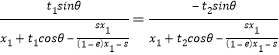
![]()
![]()
而此式恰等价于式③.故结论成立.

 阅读快车系列答案
阅读快车系列答案【题目】为了解使用手机是否对学生的学习有影响,某校随机抽取100名学生,对学习成绩和使用手机情况进行了调查,统计数据如表所示(不完整):
使用手机 | 不使用手机 | 总计 | |
学习成绩优秀 | 10 | 40 | |
学习成绩一般 | 30 | ||
总计 | 100 |
(Ⅰ)补充完整所给表格,并根据表格数据计算是否有99.9%的把握认为学生的学习成绩与使用手机有关;
(Ⅱ)现从上表不使用手机的学生中按学习成绩是否优秀分层抽样选出6人,再从这6人中随机抽取3人,记这3人中“学习成绩优秀”的人数为![]() ,试求
,试求![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】2018年8月31日,十三届全国人大常委会第五次会议表决通过了关于修改个人所得税法的决定,这是我国个人所得税法自1980年出台以来第七次大修![]() 为了让纳税人尽早享受减税红利,在过渡期对纳税个人按照下表计算个人所得税,值得注意的是起征点变为5000元,即如表中“全月应纳税所得额”是纳税者的月薪金收入减去5000元后的余额.
为了让纳税人尽早享受减税红利,在过渡期对纳税个人按照下表计算个人所得税,值得注意的是起征点变为5000元,即如表中“全月应纳税所得额”是纳税者的月薪金收入减去5000元后的余额.
级数 | 全月应纳税所得额 | 税率 |
1 | 不超过3000元的部分 |
|
2 | 超过3000元至12000元的部分 |
|
3 | 超过12000元至25000元的部分 |
|
|
|
|
某企业员工今年10月份的月工资为15000元,则应缴纳的个人所得税为______元![]()