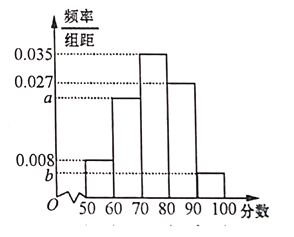
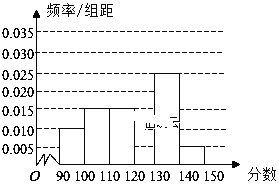
题目内容
【题目】设函数![]() ,函数
,函数![]() ,
,![]() ,其中
,其中![]() 为常数,且
为常数,且![]() ,令函数
,令函数![]() 为函数
为函数![]() 和
和![]() 的积函数.
的积函数.
(1)求函数![]() 的表达式,并求其定义域;
的表达式,并求其定义域;
(2)当![]() 时,求函数
时,求函数![]() 的值域
的值域
(3)是否存在自然数![]() ,使得函数
,使得函数![]() 的值域恰好为
的值域恰好为![]() ?若存在,试写出所有满足条件的自然数
?若存在,试写出所有满足条件的自然数![]() 所构成的集合;若不存在,试说明理由.
所构成的集合;若不存在,试说明理由.
【答案】(1)![]() 定义域为
定义域为![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)根据题意得的![]() ,再计算定义域得到答案.
,再计算定义域得到答案.
(2)设![]() ,化简得到
,化简得到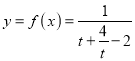 ,根据函数单调性得到值域.
,根据函数单调性得到值域.
(3)计算当![]() 时
时![]() ,且
,且![]() 时
时![]() ,根据单调性得到不等式
,根据单调性得到不等式![]() ,计算得到答案.
,计算得到答案.
(1)![]() ,定义域为
,定义域为![]()
(2)![]() ,设
,设![]()
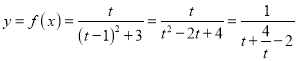
根据双勾函数性质知函数在![]() 单调递增,故
单调递增,故![]() ,故值域为
,故值域为![]()
(3)存在;根据(2)知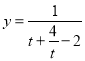 ,
,![]() ,
,
根据双勾函数性质知函数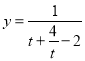 在
在![]() 单调递增,
单调递增,![]() 上单调递减.
上单调递减.
当![]() 时
时![]() ,且
,且![]() 时
时![]() ,函数
,函数![]() 的值域恰好为
的值域恰好为![]()
故![]() ,构成的集合为
,构成的集合为![]()

【题目】已知某中学高三文科班学生共有800人参加数学与地理的学业水平测试,从中随机抽取100人的数学与地理的学业水平测试成绩如下表:
人数 | 数学 | |||
优秀 | 良好 | 及格 | ||
地理 | 优秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 | a | 4 | b | |
成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩例如:表示数学成绩为良好的共有20+18+4=42(人).
(Ⅰ)若在该样本中,数学成绩优秀率为30%,求a,b的值;
(Ⅱ)已知a≥10,b≥8,利用样本数据,求数学成绩为优秀的人数比及格的人数少的概率.
【题目】新高考![]() 最大的特点就是取消文理分科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全文(选择政治、历史、地理)的选择是否与性别有关,从某学校高一年级的1000名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全文的人数比不选全文的人数少10人.
最大的特点就是取消文理分科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全文(选择政治、历史、地理)的选择是否与性别有关,从某学校高一年级的1000名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全文的人数比不选全文的人数少10人.
(1)估计在男生中,选择全文的概率.
(2)请完成下面的![]() 列联表;并估计有多大把握认为选择全文与性别有关,并说明理由;
列联表;并估计有多大把握认为选择全文与性别有关,并说明理由;
选择全文 | 不选择全文 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
附: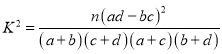 ,其中
,其中![]() .
.
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |