题目内容
8. 设函数f(x)的图象如图所示.
设函数f(x)的图象如图所示.(1)写出该函数的定义域与值域;
(2)写出该函数的最大值与最小值;
(3)写出该函数的单调区间.
分析 (1)结合函数的图象求得该函数的定义域与值域.
(2)结合函数的图象求得该函数的最值.
(3)结合函数的图象求得该函数的单调区间.
解答 解:(1)由函数f(x)的图象可得,函数的定义域为[-3,3],值域为[-1,2].
(2)函数的最大值为2,最小值为-1.
(3)结合图象,可得函数的增区间为[-3,-1],[2,3];函数的减区间为(-1,2).
点评 本题主要考查函数的图象特征,函数的定义域、值域、单调性和最值,属于基础题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
20.下列关于函数f(x)=-2sin2x-cos4x(x∈R)的说法正确的是( )
| A. | f(x)的最小正周期为2π | B. | f(x)的最大值为-1 | ||
| C. | f(x)是偶函数 | D. | f(x)在[π12,π4]上单调增 |
17.“sinA=12”是“A=30°”的( )
| A. | 充分而不必要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充分必要条件 | D. | 必要而不充分条件 |
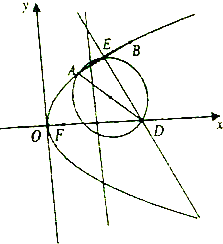 已知F(1,0)是抛物线y2=2px(p>0)的焦点.
已知F(1,0)是抛物线y2=2px(p>0)的焦点.