题目内容
【题目】设首项为1的正项数列{an}的前n项和为Sn , 且Sn+1﹣3Sn=1.
(1)求证:数列{an}为等比数列;
(2)数列{an}是否存在一项ak , 使得ak恰好可以表示为该数列中连续r(r∈N* , r≥2)项的和?请说明理由;
(3)设 ![]() ,试问是否存在正整数p,q(1<p<q)使b1 , bp , bq成等差数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
,试问是否存在正整数p,q(1<p<q)使b1 , bp , bq成等差数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
【答案】
(1)证明:∵Sn+1﹣3Sn=1,
∴当n≥2时,Sn﹣3Sn﹣1=1,
两式相减得:an+1=3an,
又∵Sn+1﹣3Sn=1,a1=1,
∴a2=S2﹣S1=2a1+1=3满足上式,
∴数列{an}是首项为1、公比为3的等比数列
(2)解:结论:不存在满足题意的项ak;
理由如下:
由(1)可知an=3n﹣1,Sn= ![]() =
= ![]() (3n﹣1),
(3n﹣1),
假设数列{an}中存在一项ak,使得ak恰好可以表示为该数列中连续r(r∈N*,r≥2)项的和,
则3k﹣1=Sr+t﹣St= ![]() (3r+t﹣1)﹣
(3r+t﹣1)﹣ ![]() (3t﹣1)=
(3t﹣1)= ![]() (3r+t﹣3t)=
(3r+t﹣3t)= ![]() 3t(3r﹣1),
3t(3r﹣1),
于是 ![]() (3r﹣1)=3x(其中x为大于1的自然数),
(3r﹣1)=3x(其中x为大于1的自然数),
整理得:3r﹣x﹣ ![]() =2,
=2,
显然r无解,故假设不成立,
于是不存在满足题意的项ak
(3)解:结论:存在唯一的数组(p,q)=(2,3)满足题意;
理由如下:
由(1)可知bn= ![]() ,
,
假设存在正整数p,q(1<p<q)使b1,bp,bq成等差数列,
则2bp=b1+bq,即2 ![]() =
= ![]() +
+ ![]() ,
,
整理得:2p3q﹣p=3q﹣1+q,
∴q=2p3q﹣p﹣3q﹣1=3q﹣p(2p﹣3p﹣1),
∵当p≥3时2p﹣3p﹣1<0,
∴当p≥3时不满足题意,
当p=2时,2 ![]() =
= ![]() +
+ ![]() 即为:
即为: ![]() =
= ![]() +
+ ![]() ,
,
整理得: ![]() =
= ![]() ,解得:q=3,
,解得:q=3,
综上所述,存在唯一的数组(p,q)=(2,3)满足题意.
【解析】(1)通过Sn+1﹣3Sn=1与Sn﹣3Sn﹣1=1作差可知an+1=3an(n≥2),进而可知数列{an}是首项为1、公比为3的等比数列;(2)通过(1)可知an=3n﹣1、Sn= ![]() (3n﹣1),假设存在满足题意的项ak , 则3k﹣1=Sr+t﹣St , 进而化简可知不存在r满足3r﹣x﹣
(3n﹣1),假设存在满足题意的项ak , 则3k﹣1=Sr+t﹣St , 进而化简可知不存在r满足3r﹣x﹣ ![]() =2,进而可得结论;(3)通过(1)可知bn=
=2,进而可得结论;(3)通过(1)可知bn= ![]() ,假设存在正整数p,q(1<p<q)使b1 , bp , bq成等差数列,通过化简可知q=3q﹣p(2p﹣3p﹣1),利用当p≥3时2p﹣3p﹣1<0可知当p≥3时不满足题意,进而验证当p=2时是否满足题意即可.
,假设存在正整数p,q(1<p<q)使b1 , bp , bq成等差数列,通过化简可知q=3q﹣p(2p﹣3p﹣1),利用当p≥3时2p﹣3p﹣1<0可知当p≥3时不满足题意,进而验证当p=2时是否满足题意即可.
【考点精析】本题主要考查了等比关系的确定和数列的前n项和的相关知识点,需要掌握等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断;数列{an}的前n项和sn与通项an的关系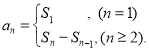 才能正确解答此题.
才能正确解答此题.

【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:

(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()