题目内容
【题目】已知双曲线E： 
﹣ 
=1（a＞0，b＞0），点F为E的左焦点，点P为E上位于第一象限内的点，P关于原点的对称点为Q，且满足|PF|=3|FQ|，若|OP|=b，则E的离心率为（ ）
A.
B.
C.2
D.
【答案】B
【解析】解：由题意可知：双曲线的右焦点F1 ， 由P关于原点的对称点为Q， 则丨OP丨=丨OQ丨，
∴四边形PFQF1为平行四边，
则丨PF1丨=丨FQ丨，丨PF丨=丨QF1丨，
由|PF|=3|FQ|，根据椭圆的定义丨PF丨﹣丨PF1丨=2a，
∴丨PF1丨=a，|OP|=b，丨OF1丨=c，
∴∠OPF1=90°，
在△QPF1中，丨PQ丨=2b，丨QF1丨=3a，丨PF1丨=a，
∴则（2b）2+a2=（3a）2 ， 整理得：b2=2a2 ，
则双曲线的离心率e= 
= 
= 
，
故选B．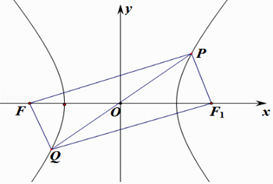
练习册系列答案
相关题目
【题目】商丘市大型购物中心——万达广场将于2018年7月6日全面开业，目前正处于试营业阶段，某按摩椅经销商为调查顾客体验按摩椅的时间，随机调查了50名顾客，体验时间（单位：分钟）落在各个小组的频数分布如下表：
体验 时间 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
（1）求这
名顾客体验时间的样本平均数
，中位数
，众数
；
（2）已知体验时间为
的顾客中有2名男性，体验时间为
的顾客中有3名男性，为进一步了解顾客对按摩椅的评价，现随机从体验时间为和的顾客中各抽一人进行采访，求恰抽到一名男性的概率．
