题目内容
【题目】如图,四边形![]() 为正方形,
为正方形,![]() 分别为
分别为![]() 的中点,以
的中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

【答案】(1)证明见解析.
(2) ![]() .
.
【解析】分析:(1)首先从题的条件中确定相应的垂直关系,即BF⊥PF,BF⊥EF,又因为![]() ,利用线面垂直的判定定理可以得出BF⊥平面PEF,又
,利用线面垂直的判定定理可以得出BF⊥平面PEF,又![]() 平面ABFD,利用面面垂直的判定定理证得平面PEF⊥平面ABFD.
平面ABFD,利用面面垂直的判定定理证得平面PEF⊥平面ABFD.
(2)结合题意,建立相应的空间直角坐标系,正确写出相应的点的坐标,求得平面ABFD的法向量,设DP与平面ABFD所成角为![]() ,利用线面角的定义,可以求得
,利用线面角的定义,可以求得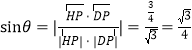 ,得到结果.
,得到结果.
详解:(1)由已知可得,BF⊥PF,BF⊥EF,又![]() ,所以BF⊥平面PEF.
,所以BF⊥平面PEF.
又![]() 平面ABFD,所以平面PEF⊥平面ABFD.
平面ABFD,所以平面PEF⊥平面ABFD.
(2)作PH⊥EF,垂足为H.由(1)得,PH⊥平面ABFD.
以H为坐标原点,![]() 的方向为y轴正方向,
的方向为y轴正方向,![]() 为单位长,建立如图所示的空间直角坐标系Hxyz.
为单位长,建立如图所示的空间直角坐标系Hxyz.

由(1)可得,DE⊥PE.又DP=2,DE=1,所以PE=![]() .又PF=1,EF=2,故PE⊥PF.
.又PF=1,EF=2,故PE⊥PF.
可得![]() .
.
则![]()
![]() 为平面ABFD的法向量.
为平面ABFD的法向量.
设DP与平面ABFD所成角为![]() ,则
,则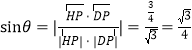 .
.
所以DP与平面ABFD所成角的正弦值为![]() .
.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案【题目】某单位为促进职工业务技能提升,对该单位120名职工进行一次业务技能测试,测试项目共5项.现从中随机抽取了10名职工的测试结果,将它们编号后得到它们的统计结果如下表(表1)所示(“√”表示测试合格,“×”表示测试不合格).
表1:
编号\测试项目 | 1 | 2 | 3 | 4 | 5 |
1 | × | √ | √ | √ | √ |
2 | √ | √ | √ | √ | × |
3 | √ | √ | √ | √ | × |
4 | √ | √ | √ | × | × |
5 | √ | √ | √ | √ | √ |
6 | √ | × | × | √ | × |
7 | × | √ | √ | √ | × |
8 | √ | × | × | × | × |
9 | √ | √ | × | × | × |
10 | √ | √ | √ | √ | × |
规定:每项测试合格得5分,不合格得0分.
(1)以抽取的这10名职工合格项的项数的频率代替每名职工合格项的项数的概率.
①设抽取的这10名职工中,每名职工测试合格的项数为![]() ,根据上面的测试结果统计表,列出
,根据上面的测试结果统计表,列出![]() 的分布列,并估计这120名职工的平均得分;
的分布列,并估计这120名职工的平均得分;
②假设各名职工的各项测试结果相互独立,某科室有5名职工,求这5名职工中至少有4人得分不少于20分的概率;
(2)已知在测试中,测试难度的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 项测试难度,
项测试难度,![]() 为第
为第![]() 项合格的人数,
项合格的人数,![]() 为参加测试的总人数.已知抽取的这10名职工每项测试合格人数及相应的实测难度如下表(表2):
为参加测试的总人数.已知抽取的这10名职工每项测试合格人数及相应的实测难度如下表(表2):
表2:
测试项目 | 1 | 2 | 3 | 4 | 5 |
实测合格人数 | 8 | 8 | 7 | 7 | 2 |
定义统计量![]() ,其中
,其中![]() 为第
为第![]() 项的实测难度,
项的实测难度,![]() 为第
为第![]() 项的预测难度(
项的预测难度(![]() ).规定:若
).规定:若![]() ,则称该次测试的难度预测合理,否则为不合理,测试前,预估了每个预测项目的难度,如下表(表3)所示:
,则称该次测试的难度预测合理,否则为不合理,测试前,预估了每个预测项目的难度,如下表(表3)所示:
表3:
测试项目 | 1 | 2 | 3 | 4 | 5 |
预测前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
判断本次测试的难度预估是否合理.
