题目内容
【题目】给定椭圆![]() :
:![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“准圆”.若椭圆
的“准圆”.若椭圆![]() 的一个焦点为
的一个焦点为![]() ,其短轴上的一个端点到
,其短轴上的一个端点到![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)设椭圆短轴的一个端点为![]() ,长轴的一个端点为
,长轴的一个端点为![]() ,点
,点![]() 是“准圆”上一动点,求三角形
是“准圆”上一动点,求三角形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ,
, ![]() .(2)
.(2)![]()
【解析】
(1)根据焦点为![]() ,短轴上的一个端点到
,短轴上的一个端点到![]() 的距离为
的距离为![]() ,得到
,得到![]() ,可得
,可得![]() ,进而可得其“准圆”方程;
,进而可得其“准圆”方程;
(2)写出直线![]() 方程,由题知要使得三角形
方程,由题知要使得三角形![]() 面积最大,则过点
面积最大,则过点![]() 的直线与直线
的直线与直线![]() 平行且于圆相切,求出过
平行且于圆相切,求出过![]() 并且与圆相切的直线,选取离直线
并且与圆相切的直线,选取离直线![]() 更远的那条直线,求出两直线的距离,利用面积公式可得三角形面积的最大值.
更远的那条直线,求出两直线的距离,利用面积公式可得三角形面积的最大值.
解:(1)由题可知![]() ,
,
![]()
![]() 椭圆方程为
椭圆方程为![]() ,
,
准圆方程为![]() .
.
(2)设椭圆短轴的一个端点为![]() ,长轴的一个端点为
,长轴的一个端点为![]() ,
,
那么直线![]() 方程为
方程为![]() ,即
,即![]()
要使得三角形![]() 面积最大,则过点
面积最大,则过点![]() 的直线与直线
的直线与直线![]() 平行且与圆相切.
平行且与圆相切.
设过点![]() 的直线
的直线![]() :
:![]() ,
,
因为直线![]() 与圆相切,所以
与圆相切,所以![]() .
.
所以![]() ,
,
当![]() 时,直线
时,直线![]() 距离直线
距离直线![]() 更远,此时三角形
更远,此时三角形![]() 面积最大,
面积最大,
即直线![]() :
:![]()
此时直线![]() 与直线
与直线![]() 的距离为
的距离为![]()
所以三角形![]() 面积最大值
面积最大值![]()

【题目】一次考试中,五名学生的数学、物理成绩如下表所示:
学生 | A1 | A2 | A3 | A4 | A5 |
数学(x分) | 89 | 91 | 93 | 95 | 97 |
物理(y分) | 87 | 89 | 89 | 92 | 93 |
(1)要从5名学生中选2人参加一项活动,求选中的学生中至少有一人的物理成绩高于90分的概率;
(2)请在所给的直角坐标系中画出它们的散点图,并求这些数据线性回归方程![]() .
.

【题目】某商家在某一天统计前5名顾客扫微信红包所得金额分别为5.9元,5.7元,4.7元,3.3元,2.1元,商家从这5名顾客中随机抽取3人赠送礼品.
(Ⅰ)求获得礼品的3人中恰好有2人的红包超过5元的概率;
(Ⅱ)商家统计一周内每天使用微信支付的人数![]() 与每天的净利润
与每天的净利润![]() (单位:元),得到如下表:
(单位:元),得到如下表:
| 12 | 16 | 22 | 25 | 26 | 29 | 30 |
| 60 | 100 | 210 | 240 | 150 | 270 | 330 |
根据表中数据用最小二乘法求![]() 与
与![]() 的回归方程
的回归方程![]() (
(![]() ,
,![]() 的计算结果精确到小数点后第二位)并估计使用微信支付的人数增加到36人时,商家当天的净利润为多少(计算结果精确到小数点后第二位)?
的计算结果精确到小数点后第二位)并估计使用微信支付的人数增加到36人时,商家当天的净利润为多少(计算结果精确到小数点后第二位)?
参考数据及公式:
①![]() ,
,![]() ;
;![]() ;
;![]()
②回归方程:![]() (其中
(其中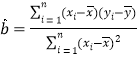 ,
,![]() )
)