题目内容
【题目】在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .设D,E分别为PA,AC中点.
.设D,E分别为PA,AC中点.
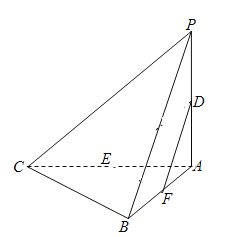
(Ⅰ)求证:![]() 平面PBC;
平面PBC;
(Ⅱ)求证:![]() 平面PAB;
平面PAB;
(Ⅲ)试问在线段AB上是否存在点F,使得过三点D,E,F的平面内的任一条直线都与平面PBC平行?若存在,指出点F的位置并证明;若不存在,请说明理由.
【答案】(Ⅰ)见证明;(Ⅱ)见证明;(Ⅲ)见解析.
【解析】
(Ⅰ)证明以DE∥平面PBC,只需证明DE∥PC;(Ⅱ)证明BC⊥平面PAB,根据线面垂直的判定定理,只需证明PA⊥BC,AB⊥BC;(Ⅲ)当点F是线段AB中点时,证明平面DEF∥平面PBC,可得平面DEF内的任一条直线都与平面PBC平行.
(Ⅰ)证明:因为点E是AC中点,点D为PA的中点,所以![]() .
.
又因为DE![]() 面PBC,PC面PBC,
面PBC,PC面PBC,
所以DE∥平面PBC.
(Ⅱ)证明:因为平面PAC⊥面ABC,平面PAC∩平面ABC=AC,又PA平面PAC,PA⊥AC,
所以PA⊥面ABC,
因为BC平面ABC,
所以PA⊥BC.
又因为AB⊥BC,且PA∩AB=A,
所以BC⊥面PAB.
(Ⅲ)
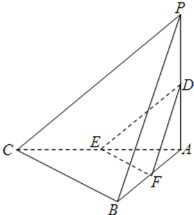
当点F是线段AB中点时,过点D,E,F的平面内的任一条直线都与平面PBC平行.
取AB中点F,连EF,连DF.
由(Ⅰ)可知DE∥平面PBC.
因为点E是AC中点,点F为AB的中点,
所以EF∥BC.
又因为EF![]() 平面PBC,BC平面PBC,
平面PBC,BC平面PBC,
所以EF∥平面PBC.
又因为DE∩EF=E,
所以平面DEF∥平面PBC,
所以平面DEF内的任一条直线都与平面PBC平行.
故当点F是线段AB中点时,过点D,E,F所在平面内的任一条直线都与平面PBC平行.

练习册系列答案
相关题目