题目内容
【题目】如图，
的内切圆于边
、
、
分别切于点
、
、
，
、
、
、
的中点分别为
、
、
、
，
与
交于点
。证明：
的外接圆与的内切圆相切。
【答案】见解析
【解析】
先证明一个结论.
若点
、
分别在
的边
、
上，且
，则
的外接圆与的外接圆相切.
证明 如图，只需考虑其中一个圆过点
的切线
，与的夹角为弦切角.
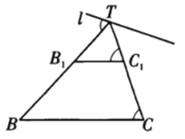
由，则
.
于是，它们同时等于弦切角.
从而，也为另一个圆的切线.故两圆切于点.
回到原题.
如图，设
的内心为
，
与
交于点
.
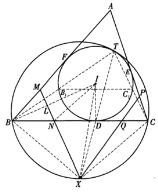
注意到，
，其中，
为内切圆
的半径.
故
等于点
对
的幂.
类似地，
等于点对的幂.
延长
，与交于点.
则
，
点在
的外接圆上.
再结合
，
平分
，设、分别与内切圆交于点、.
则
.
因为
为在点
处的切线，所以，.
而的内切圆恰为的外接圆，据所证结论，知它与的外接圆相切（因为的外接圆也为的外接圆）.
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
