题目内容
【题目】椭圆
的离心率为
，其左焦点到点
的距离为
，不过原点O的直线
与C交于A,B两点，且线段AB被直线OP平分.
（1）求椭圆C的方程；
（2）求k的值；
（3）求
面积取最大值时直线l的方程.
【答案】（1）
；（2）
；（3）
.
【解析】
（1）利用两点间的距离公式以及离心率求出
，再由
，即可求解.
（2）设
，由
，消元利用韦达定理求得线段
的中点，再根据线段的中点
在
上，可求出解.
（3）由（2）求出
，
到直线的距离，即可求得
的面积，从而问题得解.
（1）由题意可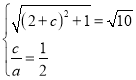得
，解得
，
，
椭圆C的方程.
（2）设，由直线
不过原点，可得
.
由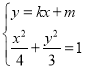 ，消元可得
①,
,
线段的中点
，
在上，易知直线的解析式为
，
，
.
（3）由（2），将①化为
，
又直线与椭圆相交，
，
，
，
又到直线的距离
，
的面积
，
令
，
则
，
，
，
取得最大值，即
取得最大值，
所求直线的方程为.
练习册系列答案
相关题目
【题目】为了调查某大学学生在某天上网的时间，随机对100名男生和100名女生进行了不记名的问卷调查. 得到如下的统计结果.
表1：男生上网时间与频数分布表：
上网时间（分钟） |
|
|
|
|
|
人数 | 10 | 20 | 40 | 20 | 10 |
表2：女生上网时间与频数分布表：
上网时间（分钟） |
|
|
|
|
|
人数 | 5 | 25 | 30 | 25 | 15 |
完成下面的2×2列联表，并回答能否有90%的把握认为“大学生上网时间与性别有关”？
附：
，其中
