题目内容
(2011•临沂二模)下面四个命题:
①函数y=
在(2,
)处的切线与直线2x-y+1=0垂直;
②已知a=∫
(sint+cost)dt,则(x-
)6展开式中的常数项为-
,
③在边长为1的正方形ABCD内(包括边界)有一点M,则△AMB的面积大于或等于
的概率为
④在一个2×2列联表中,由计算得K2=13,079,则其两个变量有关系的可能性是99.9%.
其中所有正确的命题序号是
①函数y=
| 1 |
| x |
| 1 |
| 2 |
②已知a=∫
|
| 1 |
| ax |
| 5 |
| 2 |
③在边长为1的正方形ABCD内(包括边界)有一点M,则△AMB的面积大于或等于
| 1 |
| 4 |
| 3 |
| 4 |
④在一个2×2列联表中,由计算得K2=13,079,则其两个变量有关系的可能性是99.9%.
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
②④
②④
.分析:①错,先用导数的几何意义,求出该点处切线的斜率,就可求出垂线的斜率,进而求出垂线的方程与给的不符;
②对,先用积分的知识求出a的值,然后再用二项式定理可求出常数项;
③错,点M向AB作垂线先表达出△AMB的面积,然后面积积大于或等于
,得出高应满足的条件,知道点M所在的区域,就可算出概率;
④对,根据给出的表格,通过进行值得比较就可得出变量的相关关系.
②对,先用积分的知识求出a的值,然后再用二项式定理可求出常数项;
③错,点M向AB作垂线先表达出△AMB的面积,然后面积积大于或等于
| 1 |
| 4 |
④对,根据给出的表格,通过进行值得比较就可得出变量的相关关系.
解答:解:①错,∵f′(x)=-
∴函数在(2,
)处切线的斜率k=-
= -
那么与切线垂直的直线的斜率为4,与所给的直线斜率不符合
②对,a=∫0π(sint+cost)dt=(-cost+sint)|0π=2
∴(x-
)6=(x-
)6,通项Tr+1=
x6-r(-
)r=Tr+1=
x6-2r(-
)r
又因为是常数项,所以6-2r=0,即r=3
常数项T4=
(-
)3=-
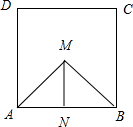
③错,如图由点M向AB作垂线,垂足为N,S△ABM=
×|AB|×|MN|=
|MN|≥
,即|MN|≥
,所以M点位于正方形的上半区域,故概率为
;
④对,∵K2=13,079>10.828,∴有两个变量有关系的可能性是99.9%
| 1 |
| x2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 4 |
那么与切线垂直的直线的斜率为4,与所给的直线斜率不符合
②对,a=∫0π(sint+cost)dt=(-cost+sint)|0π=2
∴(x-
| 1 |
| ax |
| 1 |
| 2x |
| C | r 6 |
| 1 |
| 2x |
| C | 6 r |
| 1 |
| 2 |
又因为是常数项,所以6-2r=0,即r=3
常数项T4=
| C | 3 6 |
| 1 |
| 2 |
| 5 |
| 2 |
③错,如图由点M向AB作垂线,垂足为N,S△ABM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |

④对,∵K2=13,079>10.828,∴有两个变量有关系的可能性是99.9%
点评:本题主要考查了导数的几何意义、积分、二项式定理、几何概型和独立性检验的有关知识.整体来说本题综合性比较强,所以难度中等.

练习册系列答案
相关题目
 (2011•临沂二模)如图,过圆x2+y2=4与x轴的两个交点A、B作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD与C、D两点,设AD、BC的交点为R.
(2011•临沂二模)如图,过圆x2+y2=4与x轴的两个交点A、B作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD与C、D两点,设AD、BC的交点为R. (2011•临沂二模)如图是某建筑物的三视图,现需将其外部用油漆刷一遍,若每平方米用漆0.1千克,则共需油漆大约为( )(尺寸如图,单位:米,π取3)
(2011•临沂二模)如图是某建筑物的三视图,现需将其外部用油漆刷一遍,若每平方米用漆0.1千克,则共需油漆大约为( )(尺寸如图,单位:米,π取3)